题目内容
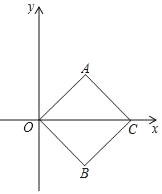
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,其中点
两点,其中点![]() 坐标为
坐标为![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.

(1)求抛物线的函数表达式;
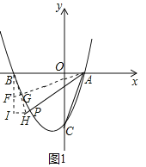
(2)如图①,连接![]() ,点
,点![]() 在抛物线上,且满足
在抛物线上,且满足![]() .求点
.求点![]() 的坐标;
的坐标;
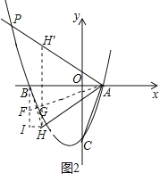
(3)如图②,点![]() 为
为![]() 轴下方抛物线上任意一点,点
轴下方抛物线上任意一点,点![]() 是抛物线对称轴与
是抛物线对称轴与![]() 轴的交点,直线
轴的交点,直线![]() 、
、![]() 分别交抛物线的对称轴于点
分别交抛物线的对称轴于点![]() 、
、![]() .请问
.请问![]() 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
【答案】(1)![]() (2)
(2)![]() 或
或![]() (3)
(3)![]() 为定值
为定值
【解析】
(1)把点![]() 、
、![]() 坐标代入抛物线解析式即求得
坐标代入抛物线解析式即求得![]() 、
、![]() 的值.
的值.
(2)点![]() 可以在
可以在![]() 轴上方或下方,需分类讨论.①若点
轴上方或下方,需分类讨论.①若点![]() 在
在![]() 轴下方,延长
轴下方,延长![]() 到
到![]() ,使
,使![]() 构造等腰
构造等腰![]() ,作
,作![]() 中点
中点![]() ,即有
,即有![]() ,利用
,利用![]() 的三角函数值,求
的三角函数值,求![]() 、
、![]() 的长,进而求得
的长,进而求得![]() 的坐标,求得直线
的坐标,求得直线![]() 的解析式后与抛物线解析式联立,即求出点
的解析式后与抛物线解析式联立,即求出点![]() 坐标.②若点
坐标.②若点![]() 在
在![]() 轴上方,根据对称性,
轴上方,根据对称性,![]() 一定经过点
一定经过点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,求得直线
,求得直线![]() 的解析式后与抛物线解析式联立,即求出点
的解析式后与抛物线解析式联立,即求出点![]() 坐标.
坐标.
(3)设点![]() 横坐标为
横坐标为![]() ,用
,用![]() 表示直线
表示直线![]() 、
、![]() 的解析式,把
的解析式,把![]() 分别代入即求得点
分别代入即求得点![]() 、
、![]() 的纵坐标,再求
的纵坐标,再求![]() 、
、![]() 的长,即得到
的长,即得到![]() 为定值.
为定值.
(1)∵抛物线![]() 经过点
经过点![]() ,
,![]() .
.
∴![]() ,解得:
,解得:![]() .
.
∴抛物线的函数表达式为![]() .
.
(2)①若点![]() 在
在![]() 轴下方,如图1,
轴下方,如图1,
延长![]() 到
到![]() ,使
,使![]() ,过点
,过点![]() 作
作![]() 轴,连接
轴,连接![]() ,作
,作![]() 中点
中点![]() ,连接并延长
,连接并延长![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
∵当![]() ,解得:
,解得:![]() ,
,![]() .
.
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() 中,
中,![]() ,
,![]() ,
,
∵![]() ,
,![]() 为
为![]() 中点,
中点,
∴![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,即
,即![]() ,
,
设直线![]() 解析式为
解析式为![]() ,
,
∴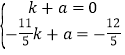 ,解得:
,解得: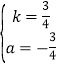 ,
,
∴直线![]() :
:![]() .
.
∵ ,解得:
,解得:![]() (即点
(即点![]() ),
),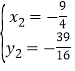 ,
,
∴![]() .
.
②若点![]() 在
在![]() 轴上方,如图2,
轴上方,如图2,
在![]() 上截取
上截取![]() ,则
,则![]() 与
与![]() 关于
关于![]() 轴对称,
轴对称,
∴![]() ,
,
设直线![]() 解析式为
解析式为![]() ,
,
∴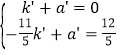 ,解得:
,解得: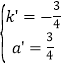 ,
,
∴直线![]() :
:![]() .
.
∵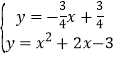 ,解得:
,解得:![]() (即点
(即点![]() ),
),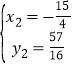 ,
,
∴![]() .
.
综上所述,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
(3)![]() 为定值.
为定值.
∵抛物线![]() 的对称轴为:直线
的对称轴为:直线![]() ,
,
∴![]() ,
,![]() ,
,
设![]() ,
,
设直线![]() 解析式为
解析式为![]() ,
,
∴![]() ,解得:
,解得:![]() ,
,
∴直线![]() :
:![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() ,
,
设直线![]() 解析式为
解析式为![]() ,
,
∴![]() ,解得:
,解得:![]() ,
,
∴直线![]() :
:![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() ,
,
∴![]() ,为定值.
,为定值.

【题目】甲、乙施工队分别从两端修一段长度为380米的公路.在施工过程中,乙队曾因技术改进而停工一天,之后加快了施工进度并与甲队共同按期完成了修路任务.下表是根据每天工程进度绘制而成的.
施工时间/天 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
累计完成施工量/米 | 35 | 70 | 105 | 140 | 160 | 215 | 270 | 325 | 380 |
下列说法错误的是( )
A. 甲队每天修路20米
B. 乙队第一天修路15米
C. 乙队技术改进后每天修路35米
D. 前七天甲,乙两队修路长度相等