题目内容
若关于x的方程(m-1)x2+2mx+m+3=0有两个不相等的实数根,则m的取值范围是 .
考点:根的判别式,一元二次方程的定义
专题:
分析:根据一元二次方程的定义和根的判别式△>0时,方程有两个不相等的实数根,建立关于m的不等式,然后求出m的取值范围;
解答:解:∵a=m-1,b=2m,c=m+3,
而方程有两个不相等的实数根,
∴△=b2-4ac=4m2-4(m-1)(m+3)>0,且m-1≠0,
∴m<
且m≠1;
故答案为:m<
且m≠1.
而方程有两个不相等的实数根,
∴△=b2-4ac=4m2-4(m-1)(m+3)>0,且m-1≠0,
∴m<
| 3 |
| 2 |
故答案为:m<
| 3 |
| 2 |
点评:此题考查了根的判别式,一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数;(3)△<0?方程没有实数根.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
计算(-2)2013+(-2)2014的结果是( )
| A、-22013 |
| B、22013 |
| C、-22014 |
| D、22014 |
某冰箱冷藏室的温度是5℃,冷冻室的温度比冷藏室的温度低17℃,则冷冻室的温度是多少摄氏度?( )
| A、12℃ | B、-12℃ |
| C、22℃ | D、-22℃ |
关于x的一元二次方程(a-1)x2+x+a2-1=0的一个根是0,则a的值为( )
| A、1 | ||
| B、-1 | ||
| C、1或-1 | ||
D、
|
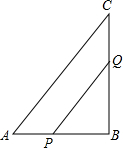 如图,在△ABC中,AB=6cm,BC=8cm,∠B=90°,点P从点A开始沿边AB向点B以1cm每秒的速度移动,与此同时,点Q从点B开始沿边BC向点C以2cm每秒的速度移动.如果P、Q分别从A、B同时出发,经过几秒,△BPQ的面积等于8cm2?
如图,在△ABC中,AB=6cm,BC=8cm,∠B=90°,点P从点A开始沿边AB向点B以1cm每秒的速度移动,与此同时,点Q从点B开始沿边BC向点C以2cm每秒的速度移动.如果P、Q分别从A、B同时出发,经过几秒,△BPQ的面积等于8cm2? 如图,DE是△ABC边AC的垂直平分线,若BC=18cm,AB=10cm,则△ABD的周长为
如图,DE是△ABC边AC的垂直平分线,若BC=18cm,AB=10cm,则△ABD的周长为 如图,△ABC与△BDE均为等腰直角三角形,BA⊥AC,DE⊥BD,点D在AB边上,连结EC,取EC中点F,求证:
如图,△ABC与△BDE均为等腰直角三角形,BA⊥AC,DE⊥BD,点D在AB边上,连结EC,取EC中点F,求证: