题目内容
3.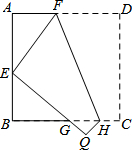 如图,将边长为16cm的正方形纸片ABCD折叠,使点D落在AB边中点E处,点C落在点Q处,折痕为FH,则线段AF的长是6cm.
如图,将边长为16cm的正方形纸片ABCD折叠,使点D落在AB边中点E处,点C落在点Q处,折痕为FH,则线段AF的长是6cm.
分析 设EF=FD=x,在RT△AEF中利用勾股定理即可解决问题.
解答 解:如图:
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=16,
∵AE=EB=8,EF=FD,设EF=DF=x.则AF=16x,
在RT△AEF中,∵AE2+AF2=EF2,
∴82+(16-x)2=x2,
∴x=10,
∴AF=16-10=6cm,
故答案为6.
点评 本题考查翻折变换、正方形的性质、勾股定理等知识,解题的关键是设未知数利用勾股定理列出方程解决问题,属于中考常考题型.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
13.方程x2-4x+4=0的根的情况是( )
| A. | 有两个相等的实数根 | B. | 只有一个实数根 | ||
| C. | 没有实数根 | D. | 有两个不相等的实数根 |
18.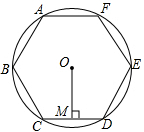 如图,已知⊙O的周长等于8πcm,则圆内接正六边形ABCDEF的边心距OM的长为( )
如图,已知⊙O的周长等于8πcm,则圆内接正六边形ABCDEF的边心距OM的长为( )
 如图,已知⊙O的周长等于8πcm,则圆内接正六边形ABCDEF的边心距OM的长为( )
如图,已知⊙O的周长等于8πcm,则圆内接正六边形ABCDEF的边心距OM的长为( )| A. | 2cm | B. | 2$\sqrt{3}$cm | C. | 4cm | D. | 4$\sqrt{3}$cm |
8.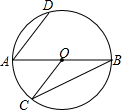 如图,AB是⊙O的直径,点C在圆周上,连结BC、OC,过点A作AD∥OC交⊙O于点D,若∠B=25°,则∠BAD的度数是( )
如图,AB是⊙O的直径,点C在圆周上,连结BC、OC,过点A作AD∥OC交⊙O于点D,若∠B=25°,则∠BAD的度数是( )
 如图,AB是⊙O的直径,点C在圆周上,连结BC、OC,过点A作AD∥OC交⊙O于点D,若∠B=25°,则∠BAD的度数是( )
如图,AB是⊙O的直径,点C在圆周上,连结BC、OC,过点A作AD∥OC交⊙O于点D,若∠B=25°,则∠BAD的度数是( )| A. | 25° | B. | 30° | C. | 40° | D. | 50° |
13.下列运算正确的是( )
| A. | a3+a3=a6 | B. | 4ab÷2a=2ab | C. | a3•a4=a7 | D. | (3x2)3=9x6 |