题目内容
3.计算:(1)$\sqrt{18}$-$\sqrt{32}$+$\sqrt{2}$
(2)6$\sqrt{6}$÷3$\sqrt{3}$×$\sqrt{32}$
(3)($\sqrt{3}$)2+(π+$\sqrt{3}$)0-$\sqrt{27}$+|$\sqrt{3}$-2|
分析 (1)原式化简后,合并同类二次根式即可得到结果;
(2)原式利用二次根式的乘除法则计算即可得到结果;
(3)原式利用平方根定义,零指数幂法则,以及绝对值的代数意义计算即可得到结果.
解答 解:(1)原式=3$\sqrt{2}$-4$\sqrt{2}$+$\sqrt{2}$=0;
(2)原式=2$\sqrt{2}$×4$\sqrt{2}$=16;
(3)原式=3+1-3$\sqrt{3}$+2-$\sqrt{3}$=6-4$\sqrt{3}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
14.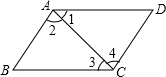 如图,要得到AB∥CD,只需要添加一个条件,这个条件不可以是( )
如图,要得到AB∥CD,只需要添加一个条件,这个条件不可以是( )
 如图,要得到AB∥CD,只需要添加一个条件,这个条件不可以是( )
如图,要得到AB∥CD,只需要添加一个条件,这个条件不可以是( )| A. | ∠1=∠3 | B. | ∠B+∠BCD=180° | C. | ∠2=∠4 | D. | ∠D+∠BAD=180° |
8.平行四边形、矩形、菱形、正方形都具有的性质是( )
| A. | 对角线互相平分 | B. | 对角线互相垂直 | ||
| C. | 对角线相等 | D. | 对角线互相垂直平分且相等 |
15.已知a2=25,$\sqrt{{b}^{2}}$=7,且|a+b|=a+b,则a-b的值为( )
| A. | 2或12 | B. | 2或-12 | C. | -2或12 | D. | -2或-12 |
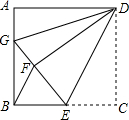 如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出下列结论:①△DAG≌△DFG;②BG=2AG;③△EBF∽△DEG;④S△BEF=$\frac{72}{5}$.其中正确结论的个数是( )
如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出下列结论:①△DAG≌△DFG;②BG=2AG;③△EBF∽△DEG;④S△BEF=$\frac{72}{5}$.其中正确结论的个数是( )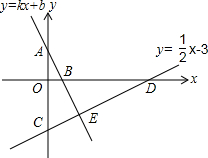 如图,点A、B的坐标分别为(0,2),(1,0),直线y=$\frac{1}{2}x$-3与坐标轴交于C、D两点.
如图,点A、B的坐标分别为(0,2),(1,0),直线y=$\frac{1}{2}x$-3与坐标轴交于C、D两点.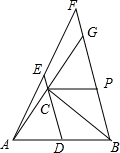 如图,△ABC中,∠C=90°,AC=3,BC=4,点D是AB的中点,点E在DC的延长线上,且CE=$\frac{1}{3}$CD,过点B作BF∥DE交AE的延长线于点F,交AC的延长线于点G.
如图,△ABC中,∠C=90°,AC=3,BC=4,点D是AB的中点,点E在DC的延长线上,且CE=$\frac{1}{3}$CD,过点B作BF∥DE交AE的延长线于点F,交AC的延长线于点G.