题目内容
如图，点C，D是以线段AB为公共弦的两条圆弧的中点，AB=4，点E，F分别是线段CD，AB上的动点，设AF=x，AE2-FE2=y，则能表示y与x的函数关系的图象是
- A.
- B.
- C.
- D.
C
分析：延长CE交AB于G，△AEG和△FEG都是直角三角形，运用勾股定理列出y与x的函数关系式即可判断出函数图象．
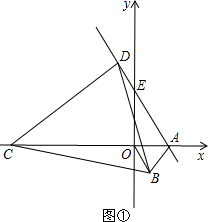
解答：
解：如右图所示，延长CE交AB于G．设AF=x，AE2-FE2=y；
∵△AEG和△FEG都是直角三角形
∴由勾股定理得：AE2=AG2+GE2，FE2=FG2+EG2，
∴AE2-FE2=AG2-FG2，即y=22-（2-x）2=-x2+4x，
这个函数是一个二次函数，抛物线的开口向下，对称轴为x=2，与x轴的两个交点坐标分别是（0，0），（4，0），顶点为（2，4），自变量0＜x＜4．
所以C选项中的函数图象与之对应．
故选C．
点评：本题为几何与函数相结合的题型，同学们应注意运用勾股定理的重要性，它就是解决此题的关键．
分析：延长CE交AB于G，△AEG和△FEG都是直角三角形，运用勾股定理列出y与x的函数关系式即可判断出函数图象．
解答：
解：如右图所示，延长CE交AB于G．设AF=x，AE2-FE2=y；∵△AEG和△FEG都是直角三角形
∴由勾股定理得：AE2=AG2+GE2，FE2=FG2+EG2，
∴AE2-FE2=AG2-FG2，即y=22-（2-x）2=-x2+4x，
这个函数是一个二次函数，抛物线的开口向下，对称轴为x=2，与x轴的两个交点坐标分别是（0，0），（4，0），顶点为（2，4），自变量0＜x＜4．
所以C选项中的函数图象与之对应．
故选C．
点评：本题为几何与函数相结合的题型，同学们应注意运用勾股定理的重要性，它就是解决此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
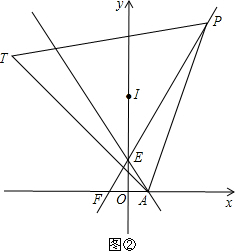
如图，点P是半圆O的直径BA延长线上的动点（不与点A重合），以PO为直径的半圆C与半圆O交于点D，∠DPB的平分线与半圆C交于点E，过E作EF⊥AB于点F，EG∥PB交PD于点G，连接GA．
如图，画线段AB的垂直平分线交AB于点O，在这条垂直平分线上截取OC=OA，以A为圆心，AC为半径画弧于AB与点P，则线段AP与AB的比是（ ）