题目内容
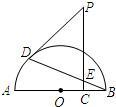
 如图,点P是半圆O的直径BA延长线上的动点(不与点A重合),以PO为直径的半圆C与半圆O交于点D,∠DPB的平分线与半圆C交于点E,过E作EF⊥AB于点F,EG∥PB交PD于点G,连接GA.
如图,点P是半圆O的直径BA延长线上的动点(不与点A重合),以PO为直径的半圆C与半圆O交于点D,∠DPB的平分线与半圆C交于点E,过E作EF⊥AB于点F,EG∥PB交PD于点G,连接GA.(1)求证:PD是半圆O的切线;
(2)若EF=
| 1 | 4 |
分析:(1)连接OD.利用圆周角定理即可推知OD⊥PD;
(2)如图2,延长OE交CD于点K,设OF=x,EF=y,由2中知,OA=OK=2OE=2y,易得四边形AFEG是矩形,有GE=AF=OA-OF=2y-x.由于GE∥AB,点E是OK的中点,则EG是△PCK的OC对的中位线,所以PO=2GE=2(2y-x),进一步得到PF=PO-OF=4y-3x,由Rt△PEF∽Rt△EOF则有EF2=CF•OF,由此得到关于x,y的方程,变形即可求出
=3或
=1,进而确定tan∠POE的值.
(2)如图2,延长OE交CD于点K,设OF=x,EF=y,由2中知,OA=OK=2OE=2y,易得四边形AFEG是矩形,有GE=AF=OA-OF=2y-x.由于GE∥AB,点E是OK的中点,则EG是△PCK的OC对的中位线,所以PO=2GE=2(2y-x),进一步得到PF=PO-OF=4y-3x,由Rt△PEF∽Rt△EOF则有EF2=CF•OF,由此得到关于x,y的方程,变形即可求出
| y |
| x |
| y |
| x |
解答: (1)证明:如图1,∵PO为直径,点D在半圆C上,
(1)证明:如图1,∵PO为直径,点D在半圆C上,
∴∠PDO=90°(直径所的对的圆周角是直角),
∴PD⊥OD.
又∵点D位于半圆O上,
∴PD是半圆O的切线;
(2)解:如图2,延长OE交CD于点K,
∵EF=
AB,
∴设OF=x,EF=y,则OA=2y,
∵GE∥CB,EF⊥CB,GA切半圆O于点A,
∴四边形AFEN是矩形,
∴GE=AF=OA-OF=2y-x;
∵PE是∠DPB的平分线,PE⊥OK,
∴点E是线段OK的中点,
∴G是PK的中点,
∴PO=2GE=2(2y-x),
∴PF=PO-OF=4y-3x,
∵EF⊥AB,PE⊥EO,
∴Rt△PEF∽Rt△EOF,
∴EF2=CF•OF,即y2=x(4y-3x),
解得,
=3或
=1,
当
=3时,tan∠POE=
=
=3,
当
=1时,点P点与点A重合,不符合题意,故舍去,
∴tan∠POE=3.
 (1)证明:如图1,∵PO为直径,点D在半圆C上,
(1)证明:如图1,∵PO为直径,点D在半圆C上,∴∠PDO=90°(直径所的对的圆周角是直角),
∴PD⊥OD.
又∵点D位于半圆O上,
∴PD是半圆O的切线;
(2)解:如图2,延长OE交CD于点K,
∵EF=
| 1 |
| 4 |
∴设OF=x,EF=y,则OA=2y,
∵GE∥CB,EF⊥CB,GA切半圆O于点A,

∴四边形AFEN是矩形,
∴GE=AF=OA-OF=2y-x;
∵PE是∠DPB的平分线,PE⊥OK,
∴点E是线段OK的中点,
∴G是PK的中点,
∴PO=2GE=2(2y-x),
∴PF=PO-OF=4y-3x,
∵EF⊥AB,PE⊥EO,
∴Rt△PEF∽Rt△EOF,
∴EF2=CF•OF,即y2=x(4y-3x),
解得,
| y |
| x |
| y |
| x |
当
| y |
| x |
| EF |
| OF |
| y |
| x |
当
| y |
| x |
∴tan∠POE=3.
点评:本题利用了圆周角定理,直径对的圆周角定理是直角,角的平分线的性质,切线的性质,矩形的判定和性质,相似三角形的判定和性质,正切的定义求解,利用的知识比较多,难度比较大.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 段PC于E,且PD=PE.
段PC于E,且PD=PE. 如图,点A是半圆上的一个三等分点,点B是弧AN的中点,点P是直径MN上一个动点,圆O的半径为1,
如图,点A是半圆上的一个三等分点,点B是弧AN的中点,点P是直径MN上一个动点,圆O的半径为1,
