题目内容
1.已知|x|=3,|y|=7.(1)求x+y的值.
(2)若x<y,求x+y的值.
分析 根据绝对值的意义得出x=±3,y=±7.
(1)分四种情况分别求出x+y的值.
(2)先由x<y得出x=3,y=7或x=-3,y=7,代入x+y即可求出答案.
解答 解:由题意知:x=±3,y=±7,
(1)分四种情况:
①如果x=3,y=7,那么x+y=3+7=10;
②如果x=3,y=-7,那么x+y=3-7=-4;
③如果x=-3,y=7,那么x+y=-3+7=4;
④如果x=-3,y=-7,那么x+y=-3-7=-10.
故x+y的值为±10或±4;
(2)∵x<y,
∴x=±3,y=7,
①如果x=3,y=7,那么x+y=3+7=10;
②如果x=-3,y=7,那么x+y=-3+7=4.
故x+y的值为10或4.
点评 本题考查绝对值的定义,代数式求值,利用分类讨论的思想是解题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
6.一元二次方程x2-4x+5=0的根的情况是( )
| A. | 方程有两个不相等的实数根 | B. | 方程有两个相等的实数根 | ||
| C. | 方程没有实数根 | D. | 不能确定 |
 如图,在△ABC中,AC的垂直平分线交BC于D,垂足为E,△ABD的周长为13cm,AC=5cm,求△ABC的周长.
如图,在△ABC中,AC的垂直平分线交BC于D,垂足为E,△ABD的周长为13cm,AC=5cm,求△ABC的周长.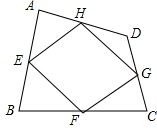 已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).