题目内容
6. 如图所示,△ABC中,AB=AC,∠A=90°,D是BC的中点,P是BC上不同于D的点,PE⊥AB于E,PF⊥AC于F.
如图所示,△ABC中,AB=AC,∠A=90°,D是BC的中点,P是BC上不同于D的点,PE⊥AB于E,PF⊥AC于F.(1)求证:DE=DF;
(2)若点P在BC的延长线上,其他条件不变,DE与DF还相等吗?若不相等,请说明理由;若相等,请给出证明.
分析 (1)连接AD,易证四边形AEPF是矩形,可得EP=AF,即可求得AF=PE=BE,即可证明△FAD≌△EBD,可得结论;
(2)连接AD,易证四边形AFPE是矩形,可得PF=AE,CF=FP,即可证明△AED≌△CFD,可得DE=DF.
解答  证明:(1)连接AD,
证明:(1)连接AD,
∵∠A=90°,PE⊥AB,PF⊥AC,
∴四边形AEPF是矩形,
∴EP=AF,
∵∠A=90°,AB=AC
∴∠CAD=∠B=45°,AD⊥BC,BD=CD,
∵PE⊥AB,
∴△BEP为等腰直角三角形,
∴PE=BE,
∴AF=PE=BE,
在△FAD和△EBD中,
$\left\{\begin{array}{l}{AF=BE}\\{∠FAD=∠B=45°}\\{AD=BD}\end{array}\right.$,
∴△FAD≌△EBD(SAS),
∴DE=DF;
(2)连接AD,
∵PE⊥AB,PF⊥AC,
∴四边形AFPE是矩形,∴PF=AE,
∵∠BAC=90°,AB=AC,
∴∠ACD=∠CAD=45°,CD=AD,AD⊥BC,
∴∠DCF=∠DAE=135°,∠FCP=45°,
∴CF=FP,
在△AED和△CFD中,
$\left\{\begin{array}{l}{AE=CF}\\{∠EAD=∠FCD}\\{AD=DC}\end{array}\right.$,
∴△AED≌△CFD(SAS),
∴DE=DF.
点评 本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证三角形全等是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,MN是线段AB的中垂线,MN=6,在MN上取C、D两点,连接AD,AC,BC,S△BMN:S△ADN=2:1,S△ADN:S△BCN=4:3,则CD的长度为$\frac{3}{4}$.
如图,MN是线段AB的中垂线,MN=6,在MN上取C、D两点,连接AD,AC,BC,S△BMN:S△ADN=2:1,S△ADN:S△BCN=4:3,则CD的长度为$\frac{3}{4}$. 如图,在四边形ABCD中,AB=AD=BC=CD=4,AB∥CD,AD∥BC,∠BAD=120°.△AEF为等边三角形,点E,F分别在BC,CD上滑动,且点E,F不与点B,C,D重合,
如图,在四边形ABCD中,AB=AD=BC=CD=4,AB∥CD,AD∥BC,∠BAD=120°.△AEF为等边三角形,点E,F分别在BC,CD上滑动,且点E,F不与点B,C,D重合,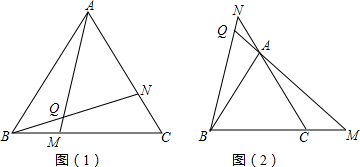
 如图,在△ABC中,AD为BC边上的中线,E为AC上一点,BE与AD交于点F,若∠FAE=∠AFE.求证:AC=BF.
如图,在△ABC中,AD为BC边上的中线,E为AC上一点,BE与AD交于点F,若∠FAE=∠AFE.求证:AC=BF. 如图,要从小河引水到村庄A,请先作出最佳路线,再写出理由:垂线段最短.
如图,要从小河引水到村庄A,请先作出最佳路线,再写出理由:垂线段最短. 如图,△ABC中,∠B=90°,点M在AB上,AM=BC,作正方形CMDE,连接AD.
如图,△ABC中,∠B=90°,点M在AB上,AM=BC,作正方形CMDE,连接AD.