题目内容
解x的方程
(1)ax+b=c(a≠0);
(2)mx-2=3x+n(m≠0);
(3)当m为何值时,方程(m2-1)x2-(m+1)x+8=0是关于x的一元一次方程,并求此时代数式(m+x)(x-2m)的值.
(1)ax+b=c(a≠0);
(2)mx-2=3x+n(m≠0);
(3)当m为何值时,方程(m2-1)x2-(m+1)x+8=0是关于x的一元一次方程,并求此时代数式(m+x)(x-2m)的值.
考点:解一元一次方程,代数式求值,一元一次方程的定义
专题:
分析:(1)移项、合并同类项,系数化成1即可求解;
(2)移项、合并同类项,系数化成1即可求解;
(3)首先根据一元一次方程的定义求得m的值,然后把m的值代入求得x的值,然后把x、m的值代入即可求得代数式的值.
(2)移项、合并同类项,系数化成1即可求解;
(3)首先根据一元一次方程的定义求得m的值,然后把m的值代入求得x的值,然后把x、m的值代入即可求得代数式的值.
解答:解:(1)移项,得:ax=c-b,
系数化成1得:x=
;
(2)移项,得:mx-3x=n+2,
合并同类项,得:(m-3)x=n+2,
系数化成1得:x=
;
(3)根据题意得:
,
解得:m=1,
则方程(m2-1)x2-(m+1)x+8=0是-2x+8=0,
解得:x=4,
则(m+x)(x-2m)=(1+4)(4-2)=10.
系数化成1得:x=
| c-b |
| a |
(2)移项,得:mx-3x=n+2,
合并同类项,得:(m-3)x=n+2,
系数化成1得:x=
| n+2 |
| m-3 |
(3)根据题意得:
|
解得:m=1,
则方程(m2-1)x2-(m+1)x+8=0是-2x+8=0,
解得:x=4,
则(m+x)(x-2m)=(1+4)(4-2)=10.
点评:本题考查解一元一次方程,解一元一次方程的一般步骤是:去分母、去括号、移项、合并同类项、化系数为1.注意移项要变号.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

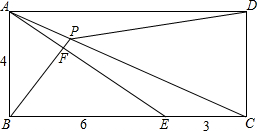 如图,在长方形ABCD中,AB=4,BE=6,EC=3,EF=2AF,BF的延长线交AC于P,则S△APD=
如图,在长方形ABCD中,AB=4,BE=6,EC=3,EF=2AF,BF的延长线交AC于P,则S△APD=