题目内容
 如图所示,以点O′(1,1)为圆心,OO′为半径画圆.判断点Q(1,0),点R(2,2)和⊙O′的位置关系.
如图所示,以点O′(1,1)为圆心,OO′为半径画圆.判断点Q(1,0),点R(2,2)和⊙O′的位置关系.
【答案】分析:点与圆的位置关系由三种情况:设点到圆心的距离为d,则当d=R时,点在圆上;当d>R时,点在圆外;当d<R时,点在圆内.
解答: 解:连接OO′,则OO′=
解:连接OO′,则OO′= =
= ,
,
点Q(1,0)在x轴上,QO′=1< ,
,
即点Q在⊙O′内;
⊙O′与x轴交于O(0,0),N(2,0),
过O′作O′M⊥NR′,则O′M=1,O′R′= ,
,
所以R′M= =1,即R′M+MN=2;
=1,即R′M+MN=2;
故R(2,2)在⊙O′上.
点评:本题主要考查了点与圆的位置关系.
解答:
 解:连接OO′,则OO′=
解:连接OO′,则OO′= =
= ,
,点Q(1,0)在x轴上,QO′=1<
 ,
,即点Q在⊙O′内;
⊙O′与x轴交于O(0,0),N(2,0),
过O′作O′M⊥NR′,则O′M=1,O′R′=
 ,
,所以R′M=
 =1,即R′M+MN=2;
=1,即R′M+MN=2;故R(2,2)在⊙O′上.
点评:本题主要考查了点与圆的位置关系.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 14、如图所示,以点O为旋转中心,将∠1按顺时针方向旋转110°得到∠2,若∠1=40°,则∠2的余角为
14、如图所示,以点O为旋转中心,将∠1按顺时针方向旋转110°得到∠2,若∠1=40°,则∠2的余角为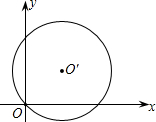 如图所示,以点O′(1,1)为圆心,OO′为半径画圆.判断点Q(1,0),点R(2,2)和⊙O′的位置关系.
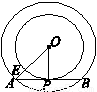
如图所示,以点O′(1,1)为圆心,OO′为半径画圆.判断点Q(1,0),点R(2,2)和⊙O′的位置关系. 如图所示,以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点,且AB=4,OP=2,连接OA交小圆于点E,则扇形EOP的面积为
如图所示,以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点,且AB=4,OP=2,连接OA交小圆于点E,则扇形EOP的面积为 按顺时针方向旋转
按顺时针方向旋转 得到
得到 ,若
,若 ,则
,则
 为圆心的两个同心圆中,大圆的弦
为圆心的两个同心圆中,大圆的弦 是小圆的切线,点
是小圆的切线,点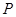 为切点,且
为切点,且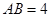 ,
,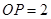 ,连结
,连结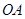 交小圆于点
交小圆于点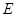 ,则扇形
,则扇形 的面积为 .
的面积为 .