题目内容
18.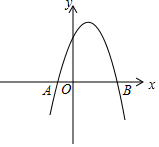 如图,在平面直角坐标系xOy中,已知抛物线y=-x2+2x+3与x轴交于A,B两点,点M在这条抛物线上,点P在y轴上,如果以点P、M、A、B为顶点的四边形是平行四边形,求点M的坐标.
如图,在平面直角坐标系xOy中,已知抛物线y=-x2+2x+3与x轴交于A,B两点,点M在这条抛物线上,点P在y轴上,如果以点P、M、A、B为顶点的四边形是平行四边形,求点M的坐标.
分析 分三种情形讨论即可.首先根据平行四边形的性质确定点M的横坐标,再利用待定系数法求出点M的坐标即可.
解答 解:如图,
∵抛物线y=-x2+2x+3与x轴交于A,B两点,
∴A(-1,0),B(3,0),
①当PM是对角线时,∵PM与AB互相平分,
∴点M的横坐标为2,
∴M(2,3).
②当PM为边时,点M在y轴的右侧,此时点M的横坐标为4,
∴M(4,-5).
③当PM为边时,点M在y轴的左侧时,此时点M的横坐标为-4,
∴M(-4,-21).
综上所述,满足条件的点M的坐标为(2,3)或(4,-5)或(-4,-21).
点评 本题考查抛物线与x轴的交点、平行四边形的判定和性质等知识,解题的关键是学会用分类讨论的首先思考问题,本题确定点M的横坐标是突破点,属于中考常考题型.

练习册系列答案
相关题目
19. 如图所示的几何体的主视图为( )
如图所示的几何体的主视图为( )
 如图所示的几何体的主视图为( )
如图所示的几何体的主视图为( )| A. |  | B. |  | C. |  | D. |  |
20.以下图形中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
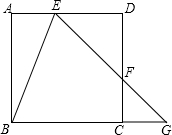 如图,正方形ABCD中,E,F分别在AD,DC上,EF的延长线交BC的延长线于G点,且∠AEB=∠BEG;
如图,正方形ABCD中,E,F分别在AD,DC上,EF的延长线交BC的延长线于G点,且∠AEB=∠BEG;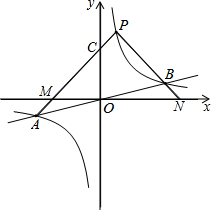 如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=$\frac{1}{4}$x的图象交于点A、B.点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=$\frac{1}{4}$x的图象交于点A、B.点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.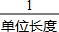 “综合与实践”学习活动准备制作一组三角形,记这些三角形的三边分别为a,b,c,并且这些三角形三边的长度为大于1且小于4的整数个单位长度.
“综合与实践”学习活动准备制作一组三角形,记这些三角形的三边分别为a,b,c,并且这些三角形三边的长度为大于1且小于4的整数个单位长度.