题目内容
9.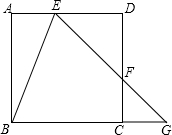 如图,正方形ABCD中,E,F分别在AD,DC上,EF的延长线交BC的延长线于G点,且∠AEB=∠BEG;
如图,正方形ABCD中,E,F分别在AD,DC上,EF的延长线交BC的延长线于G点,且∠AEB=∠BEG;(1)求证:∠ABE=$\frac{1}{2}$∠BGE;
(2)若AB=4,AE=1,求S△BEG.
分析 (1)作GM⊥BE于M.首先证明EG=GB,∠MGB=∠MGE,再证明∠ABE=∠MGB即可.
(2)求出BE、GM即可解决问题.
解答 解:(1)作GM⊥BE于M.
∵四边形ABCD是正方形,
∴AB=BC=4,∠A=∠ABC=∠BMG=90°,AD∥BG,
∵∠AEB=∠BEG,∠AEB=∠EBG,
∴∠BEG=∠EBG,
∴GE=GB,∵GM⊥EB,
∴∠MGB=∠MBE,BM=EM,
∵∠ABE+∠EBG=90°,∠EBG+∠MGB=90°,
∴∠ABE=∠MGB=$\frac{1}{2}$∠EGB.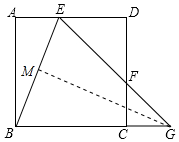
(2)在Rt△ABE中,BE=$\sqrt{A{B}^{2}+A{E}^{2}}$=$\sqrt{{4}^{2}+{1}^{2}}$=$\sqrt{17}$,∴BM=$\frac{\sqrt{17}}{2}$,
∵∠ABE=∠MGB,∠A=∠GMB=90°,
∴△ABE∽△MGB,
∴$\frac{MG}{AB}$=$\frac{BM}{AE}$,
∴$\frac{MG}{4}$=$\frac{\frac{\sqrt{17}}{2}}{1}$,
∴GM=2$\sqrt{17}$,
∴S△EBG=$\frac{1}{2}$×$\sqrt{17}$×2$\sqrt{17}$=17.
点评 本题考查正方形的性质、等腰三角形的判定和性质、相似三角形的判定和性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造相似三角形解决问题,属于中考常考题型.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
19.下列图形中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
17. 如图,将△ABC沿射线BC方向平移3cm得到△DEF.若△ABC的周长为14cm,则四边形ABFD的周长为( )
如图,将△ABC沿射线BC方向平移3cm得到△DEF.若△ABC的周长为14cm,则四边形ABFD的周长为( )
 如图,将△ABC沿射线BC方向平移3cm得到△DEF.若△ABC的周长为14cm,则四边形ABFD的周长为( )
如图,将△ABC沿射线BC方向平移3cm得到△DEF.若△ABC的周长为14cm,则四边形ABFD的周长为( )| A. | 14 cm | B. | 17 cm | C. | 20 cm | D. | 23 cm |
4.当x是怎样的实数时,$\sqrt{x-2}$在实数范围内有意义?( )
| A. | x≥3 | B. | x≥2 | C. | x≥1 | D. | x≥4 |
1.下列事件是随机事件的是( )
| A. | 在一个仅装着白球和黑球的袋中摸球,摸出红球 | |
| B. | 在一个标准大气压下,加热到100℃,水沸腾 | |
| C. | 有一名运动员奔跑的速度是30米/秒 | |
| D. | 购买一张福利彩票,中奖 |
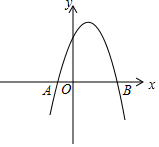 如图,在平面直角坐标系xOy中,已知抛物线y=-x2+2x+3与x轴交于A,B两点,点M在这条抛物线上,点P在y轴上,如果以点P、M、A、B为顶点的四边形是平行四边形,求点M的坐标.
如图,在平面直角坐标系xOy中,已知抛物线y=-x2+2x+3与x轴交于A,B两点,点M在这条抛物线上,点P在y轴上,如果以点P、M、A、B为顶点的四边形是平行四边形,求点M的坐标.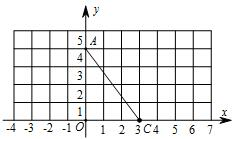 如图,在平面直角坐标系中,A(0,4),C(3,0),
如图,在平面直角坐标系中,A(0,4),C(3,0),