题目内容
已知△ABC三个内角满足：∠A：∠B：∠C=1：2：3，则△ABC是 三角形．（填锐角、直角、钝角）
考点：三角形内角和定理
专题：
分析：设∠A=x，则∠B=2x，∠C=3x，再根据三角形内角和定理求出x的值即可得出结论．
解答：解：∵△ABC三个内角满足：∠A：∠B：∠C=1：2：3，
∴设∠A=x，则∠B=2x，∠C=3x，
∵∠A+∠B+∠C=180°，即x+2x+3x=180°，解得x=30°，
∴3x=90°，
∴△ABC是直角三角形．
故答案为：直角．
∴设∠A=x，则∠B=2x，∠C=3x，
∵∠A+∠B+∠C=180°，即x+2x+3x=180°，解得x=30°，
∴3x=90°，
∴△ABC是直角三角形．
故答案为：直角．
点评：本题考查的是三角形内角和定理，熟知三角形的内角和等于180°是解答此题的关键．
练习册系列答案
名校通行证有效作业系列答案
相关题目
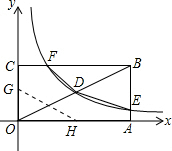如图，矩形OABC的顶点A、C分别在x、y轴的正半轴上，点D为对角线OB的中点，反比例函数y=
如图，已知正比例函数y1=x与反比例函数y2=