题目内容
随着科技的进步,高科技产品的成本在降低.某品牌的电器其成本降低8%,而零售价不变,那么利润将由以前的x%增加到(x+10)%,求x的值.
考点:一元一次方程的应用
专题:
分析:设原成本为a,售价为b,利润是x%,根据售价-成本=利润得出b-a=a•x%,整理得b=a(x%+1);现在成本降低8%,变为(1-8%)a,利润是(x+10)%,根据售价-成本=利润得出b-(1-8%)a=(1-8%)a•(x+10)%,整理得b=a[(1-8%)×(x+10)%+(1-8%)],由a≠0,得出一元一次方程x%+1=(1-8%)×(x+10)%+(1-8%),解方程即可.
解答:解:设原成本为a,售价为b,
则b-a=a•x%,即b=a(x%+1),
又因为b-(1-8%)a=(1-8%)a•(x+10)%,
即b=a[(1-8%)×(x+10)%+(1-8%)],
所以a(x%+1)=a[(1-8%)×(x+10)%+(1-8%)],
即x%+1=(1-8%)×(x+10)%+(1-8%),
解得x=15.
答:x的值为15.
则b-a=a•x%,即b=a(x%+1),
又因为b-(1-8%)a=(1-8%)a•(x+10)%,
即b=a[(1-8%)×(x+10)%+(1-8%)],
所以a(x%+1)=a[(1-8%)×(x+10)%+(1-8%)],
即x%+1=(1-8%)×(x+10)%+(1-8%),
解得x=15.
答:x的值为15.
点评:本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 如图,四边形ABCD中,过点D作DE⊥AB,作DF⊥BC,垂足分别为点E、F,∠EDF=60°,若BE=14,BF=2,求平行四边形ABCD的周长和面积.
如图,四边形ABCD中,过点D作DE⊥AB,作DF⊥BC,垂足分别为点E、F,∠EDF=60°,若BE=14,BF=2,求平行四边形ABCD的周长和面积.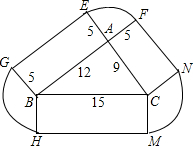 如图所示,一个房屋地基呈三角形状.三角形的边长分别为9米、12米、15米,花园由距地基边界5米之内的土地构成,问房屋连同花园共占地多少平方米?(精确到1平方米)
如图所示,一个房屋地基呈三角形状.三角形的边长分别为9米、12米、15米,花园由距地基边界5米之内的土地构成,问房屋连同花园共占地多少平方米?(精确到1平方米)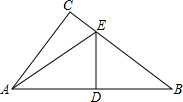 如图,在△ABC,∠C=90°,DE垂直平分斜边AB,分别交AB、BC于D、E.若∠CAE=∠B+40°,求∠AEB的度数.
如图,在△ABC,∠C=90°,DE垂直平分斜边AB,分别交AB、BC于D、E.若∠CAE=∠B+40°,求∠AEB的度数.