题目内容
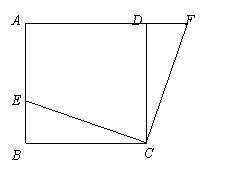
(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=B E.求证:CE=CF;
E.求证:CE=CF;
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
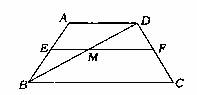
如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE=10, 求直角梯形ABCD的面积.
 |
解答:(1)证明:在正方形ABCD中,
∵BC=CD,∠B=∠CDF,BE=DF,
 ∴△CBE≌△CDF.
∴△CBE≌△CDF.
∴CE=CF.
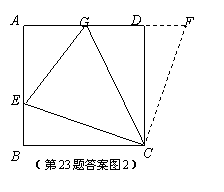
(2)证 明: 如图2,延长AD至F,使DF=BE.连接CF.
明: 如图2,延长AD至F,使DF=BE.连接CF.
由(1)知△CBE≌△CDF,
∴∠BCE=∠DCF.
∴∠BCE+∠ECD=∠DCF+∠ECD
即∠ECF=∠BCD=90°,
又∠GCE=45°,∴∠GCF=∠GCE=45°.
∵CE=CF,∠GCE=∠GCF,GC=GC,
 ∴△ECG≌△FCG.
∴△ECG≌△FCG.
∴GE=GF
∴GE=DF+GD=BE+GD.
(3)解:如图3,过C作CG⊥AD,交AD延长线于G.
在直角梯形ABCD中,
∵AD∥BC,∴∠A=∠B=9 0°,
0°,
又∠CGA=90°,AB=BC,
∴四边形ABCD 为正方形.
∴AG=BC.
已知∠DCE=45°,
 根据(1)(2)可知,ED=BE+DG.
根据(1)(2)可知,ED=BE+DG.
所以10=4+DG,即DG=6.
设AB=x,则AE=x-4,AD=x-6
在Rt△AED中, ∵ ,即
,即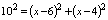 .
.
解这个方程,得:x=12,或x=-2(舍去).
∴AB=12.
所以梯形ABCD的面积为S=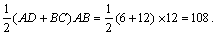
答:梯形ABCD的面积为108.

 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4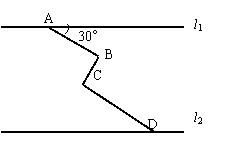
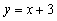 的图象与
的图象与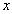 轴,
轴,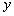 轴交于A,B两点,与反比例函数
轴交于A,B两点,与反比例函数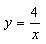 的图象相交于C,D两点,分别过C,D两点作
的图象相交于C,D两点,分别过C,D两点作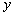 轴,
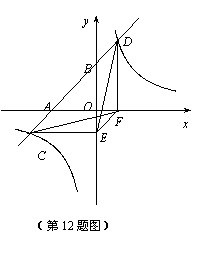
轴,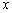 轴的垂线,垂足为E,F,连接CF,DE.有下列四个结论:
轴的垂线,垂足为E,F,连接CF,DE.有下列四个结论: .
.
 的值,其中x是不等式组
的值,其中x是不等式组 的整数解.
的整数解.



 如图,从A地到B地的公路需要经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°。因城市规划的需要,将在A,B两地之间修建一条笔直的公路。
如图,从A地到B地的公路需要经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°。因城市规划的需要,将在A,B两地之间修建一条笔直的公路。 来缩短了多少千米?
来缩短了多少千米?