题目内容
8.设实数a、b、c满足a+b+c=3,a2+b2+c2=4,求$\frac{{a}^{2}+{b}^{2}}{2+c}$+$\frac{{b}^{2}+{c}^{2}}{2+a}$+$\frac{{c}^{2}+{a}^{2}}{2+b}$的值.分析 根据已知条件得到a2+b2=4-c2,b2+c2=4-a2,a2+c2=4-b2,代入原式即可得到结论.
解答 解:∵a2+b2+c2=4,a+b+c=3,
∴a2+b2=4-c2,b2+c2=4-a2,a2+c2=4-b2,
∴原式=$\frac{4-{c}^{2}}{2+c}$+$\frac{4-{a}^{2}}{2+a}$+$\frac{4-{b}^{2}}{2+b}$
=2-c+2-a+2-b=6-(a+b+c)=3.
点评 本题考查了分式的化简求值,熟练掌握运算法则是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18. 近年来,我国很多地区持续出现雾霾天气,某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表.
近年来,我国很多地区持续出现雾霾天气,某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表.
请根据图表中提供的信息解答下列问题:
(1)m=10,n=60,扇形统计图中E组所占的百分比为15%;
(2)若该市人口约为600万人,请你估计其中持D组“观点”的市民人数;
(3)对于“雾霾”这个环境问题,请结合上面的统计情况,用简短的语言发出倡议.
 近年来,我国很多地区持续出现雾霾天气,某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表.
近年来,我国很多地区持续出现雾霾天气,某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表.| 组别 | 观点 | 频数 |
| A | 大气气压低,空气不流动 | m |
| B | 地面灰尘大,空气湿度低 | 20 |
| C | 汽车尾气排放 | n |
| D | 工厂造成的污染 | 80 |
| E | 其他 | 30 |
(1)m=10,n=60,扇形统计图中E组所占的百分比为15%;
(2)若该市人口约为600万人,请你估计其中持D组“观点”的市民人数;
(3)对于“雾霾”这个环境问题,请结合上面的统计情况,用简短的语言发出倡议.
3.2015年榕城区从中随机调查了5所初中九年级学生的数学考试成绩,学生的考试成绩情况如表(数学考试满分120分)
(1)这5所初中九年级学生的总人数有多少人?
(2)统计时,老师漏填了表中空白处的数据,请你帮老师填上;
(3)从这5所初中九年级学生中随机抽取一人,恰好是108分以上(不包括108分)的概率是多少?
| 分数段 | 频数 | 频率 |
| 72分以下 | 368 | 0.2 |
| 72----80分 | 460 | 0.25 |
| 81----95分 | 644 | 0.35 |
| 96----108分 | 184 | 0.2 |
| 109----119分 | 130 | |
| 120分 | 54 |
(2)统计时,老师漏填了表中空白处的数据,请你帮老师填上;
(3)从这5所初中九年级学生中随机抽取一人,恰好是108分以上(不包括108分)的概率是多少?
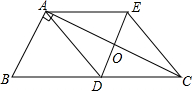 如图,在Rt△ABC中,∠BAC=90°,AD是BC边上的中线,过点D作BA的平行线交AC于点O,过点A作BC的平行线交DO的延长线于点E,连接CE.
如图,在Rt△ABC中,∠BAC=90°,AD是BC边上的中线,过点D作BA的平行线交AC于点O,过点A作BC的平行线交DO的延长线于点E,连接CE.