题目内容
抛物线y=x2+8x-9与直线x轴的交点坐标是 .
考点:抛物线与x轴的交点
专题:
分析:抛物线y=-6x2-x+2与x轴的交点的横坐标为零,即将y=0代入该函数解析式即可求得相应的x值.
解答:解:令y=0,则x2+8x-9=0,
即(x-1)(x+9)=0,
解得x1=1,x2=-9,
所以抛物线y=x2+8x-9与x轴的交点的坐标是(1,0)、(-9,0).
故答案是:(1,0)、(-9,0).
即(x-1)(x+9)=0,
解得x1=1,x2=-9,
所以抛物线y=x2+8x-9与x轴的交点的坐标是(1,0)、(-9,0).
故答案是:(1,0)、(-9,0).
点评:本题考查了抛物线与x轴的交点问题.注意将二次函数y=x2+8x-9与一元二次方程x2+8x-9=0联系起来.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
在代数式
,3-x,2x2y,
,0,
a中,单项式有( )
| m+n |
| 2 |
| 1 |
| x |
| 1 |
| 3 |
| A、4个 | B、3个 | C、2个 | D、1个 |
单项式
的系数和次数分别是( )
| 4πxy3 |
| 5 |
A、
| ||
B、
| ||
| C、4π,4 | ||
D、
|
在-4,0.3,
这四个数中,是无理数的是( )
| 2 |
| A、-4 | ||
| B、0.3 | ||
C、
| ||
D、
|
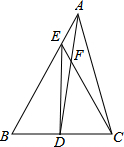 如图,在△ABC中,D为BC的中点,AD=AC,DE⊥BC,与AB相交于点E,EC与AD相交于点F,求证:
如图,在△ABC中,D为BC的中点,AD=AC,DE⊥BC,与AB相交于点E,EC与AD相交于点F,求证: 如图,已知矩形ABCD的边AB=15,BC=20.若以点A位圆心,以20为半径作⊙A,则点B、C、D与⊙A的位置关系如何?
如图,已知矩形ABCD的边AB=15,BC=20.若以点A位圆心,以20为半径作⊙A,则点B、C、D与⊙A的位置关系如何?