题目内容
8.已知:如图,在矩形ABCD中,AB=6,BC=8,对角线AC与BD交于O点,以O为顶点作∠POQ=∠ACB,∠POQ的两边分别交BC边于点P、Q(点P在点Q的左侧).(1)当OQ⊥BC时,求BP的长度;
(2)当∠POQ绕点O转动时,设BP=x,CQ=y,求y与x的函数解析式,并写出x的取值范围;
(3)联结AP,在∠POQ的转动过程中,是否存在△APO与△COQ相似?若存在,请求出这时BP的长;若不存在,请说明理由.
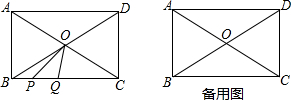
分析 (1)根据相似三角形的判定定理证明△COP∽△CBA,得到$\frac{CP}{CA}=\frac{CO}{BC}$,求出CP的长,计算即可;
(2)根据题意证明△BOQ∽△CPO,根据相似三角形的性质得到比例式计算即可;
(3)分△APO∽△COQ和△APO∽△ACP两种情况,根据相似三角形的判定和性质进行解答.
解答 解:(1)∵OQ⊥BC,
∴∠QOC+∠ACB=90°,
又∵∠POQ=∠ACB,
∴∠QOC+∠POQ=90°,
又∵∠ACB=∠PCO,
∴△COP∽△CBA,
∴$\frac{CP}{CA}=\frac{CO}{BC}$,
∴CP=$\frac{25}{4}$,
∴BP=8-$\frac{25}{4}$=$\frac{7}{4}$;
(2)∵∠BOQ=∠BOP+∠POQ,∠CPO=∠OBP+∠BOP,又∠POQ=∠OBP,
∴△BOQ∽△CPO,
∴$\frac{BQ}{CO}=\frac{BO}{CP}$,
∴y=$\frac{39-8x}{8-x}$(0≤x≤$\frac{39}{8}$);
(3)∵∠AOP=∠OQC,
当△APO∽△COQ时,∠PAO=∠ACB,即AP=CP,
(8-x)2=x2+36,
解得x=$\frac{7}{4}$;
当∠APO=∠ACB时,△APO∽△ACP,
$\frac{OA}{AP}$=$\frac{AP}{AC}$,即AP2=50,
则x2+36=50,
解得x=$\sqrt{14}$.
点评 本题考查的是相似三角形的知识的综合运用,掌握相似三角形的性质定理和判定定理是解题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
18.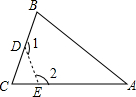 如图,从△ABC纸片中剪去△CDE,得到四边形ABDE,若∠C=60°.则∠1+∠2等于( )
如图,从△ABC纸片中剪去△CDE,得到四边形ABDE,若∠C=60°.则∠1+∠2等于( )
 如图,从△ABC纸片中剪去△CDE,得到四边形ABDE,若∠C=60°.则∠1+∠2等于( )
如图,从△ABC纸片中剪去△CDE,得到四边形ABDE,若∠C=60°.则∠1+∠2等于( )| A. | 240° | B. | 120° | C. | 230° | D. | 200° |
17.体育教师想让小强参加100米比赛,为判断他成绩是否稳定,体育教师对其10次训练成绩进行统计分析,则老师需了解小强这10次成绩的( )
| A. | 众数 | B. | 中位数 | C. | 平均数 | D. | 方差 |

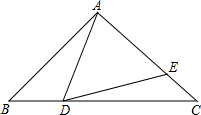 △ABC中,AB=AC=3,∠B=30°,点D在直线BC上运动(D与B、C不重合)连AD,作∠ADE=30°,DE交AC于E.
△ABC中,AB=AC=3,∠B=30°,点D在直线BC上运动(D与B、C不重合)连AD,作∠ADE=30°,DE交AC于E. 已知:BC∥EF,∠B=∠E,求证:AB∥DE.
已知:BC∥EF,∠B=∠E,求证:AB∥DE. 如图,反比例函数y=$\frac{k}{x}$的图象经过点(5,4),若y>4,则x的取值范围是0<x<5.
如图,反比例函数y=$\frac{k}{x}$的图象经过点(5,4),若y>4,则x的取值范围是0<x<5.