题目内容
已知A（-1，y1），B（-2，y2）都在抛物线y=3x2上，则y1与y2之间的大小关系是（ ）
| A、y1＞y2 |
| B、y1＜y2 |
| C、y1=y2 |
| D、不能确定大小关系 |
考点：二次函数图象上点的坐标特征
专题：
分析：先求得函数y=3x2上的对称轴为y轴，再判断A（-1，y1）、B（-2，y2）在对称轴左侧，从而判断出y1与y2的大小关系．
解答：解：∵函数y=3x2上的对称轴为y轴，
∴A（-1，y1）、B（-2，y2）在对称轴左侧，
∴抛物线开口向上，对称轴左侧y随x的增大而减小．
∵-1＞-2
∴y1＜y2．
故选B
∴A（-1，y1）、B（-2，y2）在对称轴左侧，
∴抛物线开口向上，对称轴左侧y随x的增大而减小．
∵-1＞-2
∴y1＜y2．
故选B
点评：此题主要考查了二次函数图象上点的特征，利用已知解析式得出对称轴进而利用二次函数增减性得出是解题关键．
练习册系列答案
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
如图，点A的坐标是（3，3），点P在坐标轴上，且△APO是等腰三角形，则点P的坐标位置有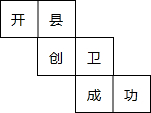
小林同学在正方体盒子的每个面上都写了一个字，分别是开、县、创、卫、成、功，其平面展开图如图所示，那么该正方体盒子上，“开”相对的面上所写的文字是
如图，⊙O1、⊙O2内切于点A，其半径分别是2和1，将⊙O2沿直线O1O2平移至两圆内切时，则点O2移动的长度是下列函数是二次函数的是（ ）
A、y=
| ||
B、y=
| ||
C、y=
| ||
| D、y=3x2+6x-5 |