题目内容
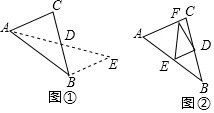
10.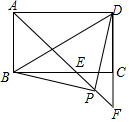 在矩形ABCD中,∠DAB的平分线交BC于点E,交DC的延长线于点F,连接BD.
在矩形ABCD中,∠DAB的平分线交BC于点E,交DC的延长线于点F,连接BD.(1)直接写出∠AEC的度数(不需证明);
(2)求证:BE=DC;
(3)点P是线段EF上一动点(不与点E,F重合),在点P运动过程中,能否△BDP成为等腰直角三角形?若能,写出点P满足的条件并证明;若不能,请说明理由.
分析 (1)由矩形的性质与三角形外角和定理即可得出结果;
(2)由矩形的性质得出AB=DC、AD∥BC,再平行线的性质得出∠AEB=∠EAD=45°,即可得出结论;
(3)连接CP,证出△CEF为等腰直角三角形,再由点P是线段EF的中点得出EP=CP、∠ECP=45°、∠EPC=90°,由SAS证得△BEP≌△DCP,即可得出结论.
解答 (1)解:∵四边形ABCD时矩形,
∴∠DAB=∠ABC=∠DCB=90°,
∵∠DAB的平分线交BC于点E,
∴∠BAE=∠EAD=45°,
∴∠AEC=∠ABC+∠BAE=90°+45°=135°;
(2)证明:∵四边形ABCD时矩形,
∴AB=DC,AD∥BC,
∴∠AEB=∠EAD=45°,
∴∠BAE=∠AEB=45°,
∴AB=BE,
∴BE=DC;
(3)解:在点P运动过程中,能使△BDP成为等腰直角三角形,此时点P是线段EF的中点;理由如下:
连接CP,如图所示:
∵四边形ABCD时矩形,DC的延长线于点F,
∴∠ECF=90°,AB∥DF,
∴∠F=∠BAE=45°,
∵∠FEC=∠AEB=45°,
∴∠F=∠FEC,
∴CE=CF,
∵点P是线段EF的中点,
∴EP=CP,∠ECP=45°,∠EPC=90°,
∴∠DCP=∠DCB+∠ECP=90°+45°=135°,
∵∠BEP=∠AEC=135°,
∴∠BEP=∠DCP,
在△BEP和△DCP中,$\left\{\begin{array}{l}{BE=DC}\\{∠BEP=∠DCP}\\{EP=CP}\end{array}\right.$,
∴△BEP≌△DCP(SAS),
∴BP=DP,∠BPE=∠DPC,
∴∠BPD=∠BPE+∠DPE=∠DPC+∠DPE=∠EPC=90°,
∴△BDP为等腰直角三角形.
点评 本题是四边形综合题目,考查了矩形的性质、平行线的性质、等腰三角形的判定与性质、等腰直角三角形的判定与性质、全等三角形的判定与性质、三角形外角和定理等知识;熟练掌握等腰三角形与等腰直角三角形的判定与性质是解决问题的关键.

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |

| A. | (1)(2)(3) | B. | (2)(3)(4) | C. | (3)(4)(5) | D. | (1)(2)(5) |
| A. | 两条射线 | B. | 两条直线 | C. | 直线与射线 | D. | 两条线段 |
| A. | 对角线互相平分的四边形是平行四边形 | |
| B. | 两组对角分别相等的四边形是平行四边形 | |
| C. | 一组对边平行,另一组对边相等的四边形是平行四边形 | |
| D. | 对角线相等的平行四边形是矩形 |
| A. | p-q | B. | q-p | C. | -p-q | D. | p+q |
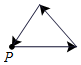
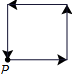
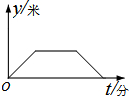 李阿姨每天早晨从家慢跑道小区公园,锻炼一阵后,再慢跑回家.表示李阿姨离开家的距离y (单位:米)与时间t (单位:分)的函数关系的图象大致如上图所示,则李阿姨跑步的路线可能是(用P点表示李阿姨家的位置)( )
李阿姨每天早晨从家慢跑道小区公园,锻炼一阵后,再慢跑回家.表示李阿姨离开家的距离y (单位:米)与时间t (单位:分)的函数关系的图象大致如上图所示,则李阿姨跑步的路线可能是(用P点表示李阿姨家的位置)( )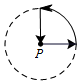
 (1)阅读理解:
(1)阅读理解: 如图所示的计算程序中,y与x之间的函数关系所对应的图象应为( )
如图所示的计算程序中,y与x之间的函数关系所对应的图象应为( )


