题目内容
16.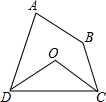 如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线交于点O,则∠COD的度数为( )
如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线交于点O,则∠COD的度数为( )| A. | 135° | B. | 120° | C. | 110° | D. | 100° |
分析 首先根据四边形内角和可得∠ADC+∠DCB=360°-200°=160°,再根据角平分线的性质可得∠ODC+∠OCD=$\frac{1}{2}$×160°=80°,再进一步利用三角形内角和定理可得答案.
解答 解:∵四边形ABCD中,∠A+∠B=200°,
∴∠ADC+∠DCB=360°-200°=160°,
∵∠ADC、∠DCB的平分线相交于点O,
∴∠ODC=$\frac{1}{2}$∠ADC,∠OCD=$\frac{1}{2}∠$BCD,
∴∠ODC+∠OCD=$\frac{1}{2}$×160°=80°,
∴∠COD=180°-80°=100°,
故选D
点评 此题主要考查了多边形内角和定理,关键是掌握多边形内角和定理:(n-2).180 (n≥3)且n为整数).

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
7.如图是临沭县某天六个整点时的气温绘制成的统计图,则这六个整点时气温的中位数是( )


| A. | 15.3℃ | B. | 19.6℃ | C. | 17.45℃ | D. | 15.6℃ |
8.下列语句不正确的是( )
| A. | 直角三角形斜边上的中线等于连结两直角边的中点的中位线 | |
| B. | 对角线相等且垂直的四边形是正方形 | |
| C. | 角平分线上任意一点与每条边上到顶点的距离相等的点的连线段相等 | |
| D. | 顺次连结对角线垂直的四边形各边中点的四边形是矩形 |