题目内容
18. 如图,在?ABCD中对角线AC,BD相交于点O,∠1=∠2,试判断四边形ABCD的形状,并证明你的结论.
如图,在?ABCD中对角线AC,BD相交于点O,∠1=∠2,试判断四边形ABCD的形状,并证明你的结论.
分析 先由四边形ABCD是平行四边形,根据平行四边形的对角线互相平分得出AC=2OC,BDE=2OB,再由∠1=∠2,根据等角对等边得出OC=OB,那么AC=BD,根据对角线相等的平行四边形是矩形得出?ABCD是矩形.
解答 解:四边形ABCD是矩形,理由如下:
∵四边形ABCD是平行四边形,
∴AC=2OC,BDE=2OB,
∵∠1=∠2,
∴OC=OB,
∴AC=BD,
∴?ABCD是矩形.
点评 本题考查了矩形的判定,判定一个四边形是矩形有三种方法:①矩形的定义:有一个角是直角的平行四边形是矩形;②有三个角是直角的四边形是矩形;
③对角线相等的平行四边形是矩形(或“对角线互相平分且相等的四边形是矩形”).也考查了平行四边形和等腰三角形的性质.

练习册系列答案
相关题目
8.下列运算中,错误的是( )
| A. | $\sqrt{2}$×$\sqrt{5}$=$\sqrt{10}$ | B. | $\sqrt{1{6}^{2}+{9}^{2}}$=16+9=25 | ||
| C. | 2$\sqrt{2}$+3$\sqrt{2}$=5$\sqrt{2}$ | D. | $\sqrt{27}$÷$\sqrt{3}$=3 |
8.一个不透明的袋中装有除颜色外,其余均相同的5个红球和2个黄球,从中随机摸出一个,摸到红球的概率是 ( )
| A. | $\frac{1}{7}$ | B. | $\frac{1}{5}$ | C. | $\frac{5}{7}$ | D. | $\frac{2}{5}$ |
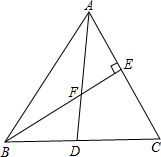 如图,锐角△ABC中.AD是∠BAC的平分线.线段BE垂直AC于E点.交线段AD于F.
如图,锐角△ABC中.AD是∠BAC的平分线.线段BE垂直AC于E点.交线段AD于F.