Question

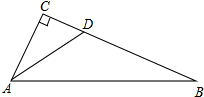如图，在Rt△ABC中，∠C=90°，AD是∠BAC的平分线，且AD=BD，DC=2，求BC的长．

Answer 1

考点：角平分线的性质,勾股定理

专题：

分析：如图，首先证明∠CAD=∠BAD=α；证明∠DAB=∠B=α；根据直角三角形的两锐角互余，求出∠CAD=30°，求出AD的长，即可解决问题．

解答：解：∵AD是∠BAC的平分线，
∴∠CAD=∠DAB（设为α）；
又∵AD=BD，
∴∠DAB=∠B=α；
∵∠C=90°，
∴∠CAB+∠B=90°，即3α=90°，
∴∠CAD=30°，sin30°=

CD

AD

=

2

AD

，
∴AD=4，BC=2+4=6．

点评：该题主要考查了角平分线的定义、直角三角形的性质、直角三角形的边角关系等几何知识点问题；解题的关键是灵活运用有关定理来分析、判断、推理或解答．