题目内容
17.若一次函数y=(1+2k)x+(2k-1)是正比例函数,则k=$\frac{1}{2}$.分析 根据正比例函数的定义可得:比例系数1+2k≠0,且2k-1=0,再解即可.
解答 解:由题意得:1+2k≠0,2k-1=0,
解得:k=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 此题主要考查了正比例函数的定义,关键是掌握形如y=kx(k是常数,k≠0)的函数叫做正比例函数,其中k叫做比例系数.

练习册系列答案
相关题目
5.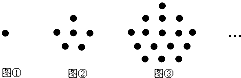 如图图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有1颗棋子,第②个图形一共有6颗棋子,第③个图形一共有16颗棋子,…,则第⑧个图形中棋子的颗数为( )
如图图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有1颗棋子,第②个图形一共有6颗棋子,第③个图形一共有16颗棋子,…,则第⑧个图形中棋子的颗数为( )
 如图图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有1颗棋子,第②个图形一共有6颗棋子,第③个图形一共有16颗棋子,…,则第⑧个图形中棋子的颗数为( )
如图图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有1颗棋子,第②个图形一共有6颗棋子,第③个图形一共有16颗棋子,…,则第⑧个图形中棋子的颗数为( )| A. | 141 | B. | 106 | C. | 169 | D. | 150 |
7.已知代数式m-n+1的值是8,那么代数式4m-4n+1的值是( )
| A. | 37 | B. | 25 | C. | 29 | D. | 0 |
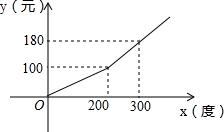 为增加公民的节约用电意识,某市采用分段计费的方法按月计算每户家庭的电费.每户家庭每月电费y(元)与用电量x(度)之间的函数图象如图所示.
为增加公民的节约用电意识,某市采用分段计费的方法按月计算每户家庭的电费.每户家庭每月电费y(元)与用电量x(度)之间的函数图象如图所示.