题目内容
9.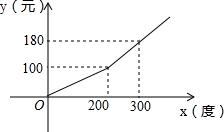 为增加公民的节约用电意识,某市采用分段计费的方法按月计算每户家庭的电费.每户家庭每月电费y(元)与用电量x(度)之间的函数图象如图所示.
为增加公民的节约用电意识,某市采用分段计费的方法按月计算每户家庭的电费.每户家庭每月电费y(元)与用电量x(度)之间的函数图象如图所示.(1)若甲用户某月用电量为150度,则该月应缴电费75元.
(2)求y与x之间的函数关系式.
(3)若乙用户某月需缴电费132元,求乙用户该月的用电量.
分析 (1)根据图象可以得到0≤x≤200时的函数解析式,从而可以解答本题;
(2)根据图象可以分别设出0≤x≤200,x>200时的函数解析式,从而可以解答本题;
(3)根据图象可以判断电费132元在x>200的函数图象上,从而可以解答本题.
解答 解:(1)根据图象可得,
0≤x≤200时,设y=kx.
则100=200k.
解得,k=0.5.
0≤x≤200时,y=0.5x.
∴x=150时,y=0.5×150=75(元).
故答案为:75.
(2)根据图象可得,
0≤x≤200时,设y=kx.
则100=200k.
解得,k=0.5.
0≤x≤200时,y=0.5x.
当x>200时,设y=mx+b.
则$\left\{\begin{array}{l}{100=200m+b}\\{180=300m+b}\end{array}\right.$.
解得m=0.8,b=-60.
∴x>200时,y=0.8x-60.
由上可得,y与x之间的函数关系式是:y=$\left\{\begin{array}{l}{0.5x(0≤x≤200)}\\{0.8x-60(x>200)}\end{array}\right.$.
(3)将y=132代入y=0.8x-60得,x=240.
即乙用户某月需缴电费132元,乙用户该月的用电量是240度.
点评 本题考查一次函数的应用,解题的关键是利用数形结合的数学思想,将图象与实际问题联系在一起,然后找出所求问题需要的条件.

练习册系列答案
相关题目
19.下列各组数据中,结果相等的是( )
| A. | (-1)4与-14 | B. | -|-3|与-(-3) | C. | ${\frac{2}{3}^2}与{({\frac{2}{3}})^2}$ | D. | ${({\frac{-1}{3}})^3}与\frac{-1}{3^3}$ |
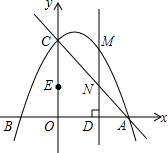 如图,抛物线y=-$\frac{1}{2}{x}^{2}+bx+c$经过A(4,0),C(0,4)两点,点B是抛物线与x轴的另一个交点,点E是OC的中点,作直线AC、点M在抛物线上,过点M作MD⊥x轴,垂足为点D,交直线AC于点N,设点M的横坐标为m,MN的长度为d.
如图,抛物线y=-$\frac{1}{2}{x}^{2}+bx+c$经过A(4,0),C(0,4)两点,点B是抛物线与x轴的另一个交点,点E是OC的中点,作直线AC、点M在抛物线上,过点M作MD⊥x轴,垂足为点D,交直线AC于点N,设点M的横坐标为m,MN的长度为d.
 由4个相同的小立方体搭成的几何体如图所示,则从正面看到的几何体的形状是( )
由4个相同的小立方体搭成的几何体如图所示,则从正面看到的几何体的形状是( )


