题目内容
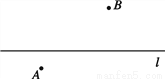
如图,已知直线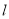 及其两侧两点A、B. (要求:保留作图痕迹,不需要证明)
及其两侧两点A、B. (要求:保留作图痕迹,不需要证明)
(1)在直线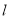 上求一点P,使PA=PB;
上求一点P,使PA=PB;
(2)在直线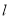 上求一点Q,使
上求一点Q,使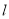 平分∠AQB.
平分∠AQB.
练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
题目内容
如图,已知直线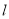 及其两侧两点A、B. (要求:保留作图痕迹,不需要证明)
及其两侧两点A、B. (要求:保留作图痕迹,不需要证明)
(1)在直线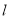 上求一点P,使PA=PB;
上求一点P,使PA=PB;
(2)在直线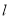 上求一点Q,使
上求一点Q,使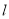 平分∠AQB.
平分∠AQB.

 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案