题目内容
10.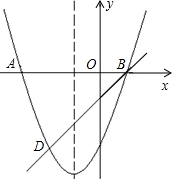 如图,二次函数y=x2+bx+c的图象与x轴交于A、B两点,且A点坐标为(-3,0),经过B点的直线交抛物线于点D(-2,-3).
如图,二次函数y=x2+bx+c的图象与x轴交于A、B两点,且A点坐标为(-3,0),经过B点的直线交抛物线于点D(-2,-3).(1)求抛物线的解析式;
(2)过x轴上点E(a,0)(E点在B点的右侧)作直线EF∥BD,交抛物线于点F,求直线BD和直线EF的解析式;
(3)是否存在实数a使四边形BDFE是平行四边形?如果存在,求出满足条件的a;如果不存在,请说明理由.
分析 (1)将A、D两点的坐标代入解析式求出b、c即可;
(2)先求出B点坐标,再根据B、D两点坐标求出BD解析式,进而求出EF解析式;
(3)由于EF已经与BD平行了,只需让DF∥BE就可以了,此时,F点的纵坐标与D点相同,从而可求出F点的坐标,进而求出E点坐标,即求出a的值.
解答 解:(1)将A、D两点代入y=x2+bx+c可求得:b=2,c=-3,
∴抛物线解析式为y=x2+2x-3
(2)由抛物线解析式y=x2+2x-3可求B的坐标是(1,0),
由B、D两点坐标求得直线BD的解析式为y=x-1;
∵EF∥BD,
∴直线EF的解析式为:y=x-a
(3)若四边形BDFE是平行四边形,则DF∥x轴,如图,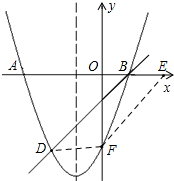
∴D、F两点的纵坐标相等,即点F的纵坐标为-3.
∴F点的坐标为(0,-3),
∴DF=2,
∴BE=DF=2,
∴E(3,0),
即:a=3.
所以存在实数a=3,使四边形BDFE是平行四边形.
点评 本题是二次函数综合题,主要考查了待定系数法求二次函数解析式、抛物线与x轴的交点坐标、待定系数法求直线解析式、平行四边形的判定与性质等知识点,虽有一定综合性,但难度不大,属于较基础的题.

练习册系列答案
相关题目
20.圆锥的侧面展开图是( )
| A. | 扇形 | B. | 等腰三角形 | C. | 圆 | D. | 矩形 |
2.如图,图①由4个正三角形和3个正六边形拼成,图②由8个正三角形和5个正六边形拼成,图③由12个正三角形和7个正六边形拼成,依次规律,则第n个图案中,正三角形和正六边形的个数分别是( )


| A. | n2+n+2,2n+1 | B. | 2n+2,2n+1 | C. | 4n,n2-n+3 | D. | 4n,2n+1 |
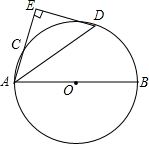 如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D垂直于AC的直线交AC的延长线于点E.
如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D垂直于AC的直线交AC的延长线于点E.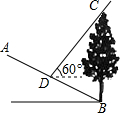 如图,斜坡AB的坡度i=1:2,坡脚B处有一棵树BC,某一时刻测得树BC在斜坡AB上的影子BD的长度为10米,这时测得太阳光线与水平线的夹角为60°,则树BC的高度为2$\sqrt{5}$+4$\sqrt{15}$米.
如图,斜坡AB的坡度i=1:2,坡脚B处有一棵树BC,某一时刻测得树BC在斜坡AB上的影子BD的长度为10米,这时测得太阳光线与水平线的夹角为60°,则树BC的高度为2$\sqrt{5}$+4$\sqrt{15}$米.
 如图,5个一样大小的小长方形拼成一个大长方形ABCD,如果大长方形ABCD的周长为14cm,求小长形的长和宽.
如图,5个一样大小的小长方形拼成一个大长方形ABCD,如果大长方形ABCD的周长为14cm,求小长形的长和宽.