题目内容
 如图,已知△ABD和△CEF是斜边为2cm的全等直角三角形,其中∠ABD=∠FEC=60°,且B,D,C,E在同一直线上,DC=4.△ABD沿着BE的方向以每秒1cm的速度运动,设△ABD运动时间为t秒.
如图,已知△ABD和△CEF是斜边为2cm的全等直角三角形,其中∠ABD=∠FEC=60°,且B,D,C,E在同一直线上,DC=4.△ABD沿着BE的方向以每秒1cm的速度运动,设△ABD运动时间为t秒.①当t为何值时,平行四边形ABFE是菱形?
②平行四边形ABFE可能是矩形吗?若可能,求出t的值和矩形的面积;若不可能,请说明理由.
考点:矩形的判定与性质,菱形的判定
专题:动点型
分析:①由△ABD和△CEF是斜边为2cm的全等直角三角形,易证得平行四边形ABFE是平行四边形;即可得当点D与点C重合时,四边形ABFE是菱形,则可求得t的值;
②由当四边形ABFE是矩形时,可得∠BAE=90°,又由∠ABD=∠FEC=60°,即可求得答案.
②由当四边形ABFE是矩形时,可得∠BAE=90°,又由∠ABD=∠FEC=60°,即可求得答案.
解答: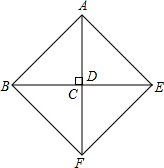 解:①如图,当点D与点C重合时,四边形ABFE是菱形,
解:①如图,当点D与点C重合时,四边形ABFE是菱形,
∵Rt△ABD≌Rt△FEC,
∴AB=EF,∠ABD=∠FEC,
∴AB∥EF,
∴平行四边形ABFE是平行四边形;
∵AD⊥BE,CF⊥BE,
∴AF⊥BE,
∴四边形ABFE是菱形,
∵DC=4,
∴△ABD运动的距离为4cm,
∴t=4;
②能.
 当四边形ABFE是矩形时,∠BAE=90°,
当四边形ABFE是矩形时,∠BAE=90°,
∴∠BEA=90°-60°=30°,
∵AB=2cm,
∴BE=2AB=4cm,BD=1cm,
∴C′D′=4-1-1=2(cm),AE=
=2
(cm),
∴t=2,S矩形ABFE=2S△ABE=2×
×2×2
=4
(cm2).
 解:①如图,当点D与点C重合时,四边形ABFE是菱形,
解:①如图,当点D与点C重合时,四边形ABFE是菱形,∵Rt△ABD≌Rt△FEC,
∴AB=EF,∠ABD=∠FEC,
∴AB∥EF,
∴平行四边形ABFE是平行四边形;
∵AD⊥BE,CF⊥BE,
∴AF⊥BE,
∴四边形ABFE是菱形,
∵DC=4,
∴△ABD运动的距离为4cm,
∴t=4;
②能.
 当四边形ABFE是矩形时,∠BAE=90°,
当四边形ABFE是矩形时,∠BAE=90°,∴∠BEA=90°-60°=30°,
∵AB=2cm,
∴BE=2AB=4cm,BD=1cm,
∴C′D′=4-1-1=2(cm),AE=
| BE2-AB2 |
| 3 |
∴t=2,S矩形ABFE=2S△ABE=2×
| 1 |
| 2 |
| 3 |
| 3 |
点评:此题考查了矩形的判定与性质、菱形的判定与性质以及全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
 一块玻璃,AB∥CD,玻璃的板部分被打碎了,小华知道这块玻璃的高与CD相同,请画出打碎前的图形,并写出画法.
一块玻璃,AB∥CD,玻璃的板部分被打碎了,小华知道这块玻璃的高与CD相同,请画出打碎前的图形,并写出画法.
 如图所示,四边形ABCD是菱形,AC,BD是对角线,∠ABC=30°.求证:AB2=AC•BD.
如图所示,四边形ABCD是菱形,AC,BD是对角线,∠ABC=30°.求证:AB2=AC•BD.