题目内容
已知正六边形的内切圆的半径是
，则正六边形的半径为 ．
| 3 |
考点：正多边形和圆
专题：
分析：根据题意画出图形，利用正六边形中的等边三角形的性质求解即可．
解答：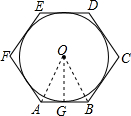
解：如图，连接OA、OB，OG；
∵六边形ABCDEF是边长等于正六边形的半径，设正六边形的半径为a，
∴△OAB是等边三角形，
∴OA=AB=a，
∴OG=OA•sin60°=a×
=
，
解得：a=2，
∴边长为a的正六边形的半径为：2．
故答案为：2．
解：如图，连接OA、OB，OG；∵六边形ABCDEF是边长等于正六边形的半径，设正六边形的半径为a，
∴△OAB是等边三角形，
∴OA=AB=a，
∴OG=OA•sin60°=a×
| ||
| 2 |
| 3 |
解得：a=2，
∴边长为a的正六边形的半径为：2．
故答案为：2．
点评：此题主要考查了正多边形、等边三角形及特殊角的三角函数值，根据已知得出六边形ABCDEF是边长等于正六边形的半径是解题关键．
练习册系列答案
相关题目
如图，直线y=ax+b经过A（-2，-5）、B（3，0）两点，那么，不等式组2（ax+b）＜5x＜0的解集是已知点(a，
)是y=kx与y=-
两函数图象的一个交点．则k=（ ）
| 3 |
| ||
| x |
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|
如图，正方形A1B1C1D1可看成是分别以A、B、C、D为位似中心将正方形ABCD放大一倍得到的图形（正方形ABCD的边长放大到原来的3倍），由正方形ABCD到正方形A1B1C1D1，我们称之作了一次变换，再将正方形A1B1C1D1作一次变换就得到正方形A2B2C2D2，…，依此下去，作了2005次变换后得到正方形A2005B2005C2005D2005，若正方形ABCD的面积是1，那么正方形A2005B2005C2005D2005的面积是多少（ ）