题目内容
15.在平面直角坐标系中有两点A(2,4)、B(1,1),在y轴上有一点C,使AC+BC距离最短,则C点的坐标是(0,2).分析 作点A(2,4)关于y轴的对称点D,连接BD交y轴于C,则BD的长就是AC+BC距离的最小值,根据对称的性质得到A(2,4)关于y轴的对称点D(-2,4),求得直线BD的解析式为:y=-x+2,即可得到结论.
解答 解:作点A(2,4)关于y轴的对称点D,连接BD交y轴于C,
则BD的长就是AC+BC距离的最小值,
∵A(2,4)关于y轴的对称点D(-2,4),
设直线BD的解析式为:y=kx+b,
∴$\left\{\begin{array}{l}{1=k+b}\\{4=-2k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=2}\end{array}\right.$,
∴直线BD的解析式为:y=-x+2,
令x=0,则y=2,
∴C(0,2),
故答案为:(0,2).
点评 本题考查了轴对称-路径最短问题,关键是通过对称找到最短路径.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
5.下列方程中是关于x的一元二次方程的是( )
| A. | ax2+bx+c=0 | B. | $\frac{1}{{x}^{2}}$+$\frac{2}{x}$=3 | C. | x2+2x=x2-1 | D. | 2(x-1)2=2(x+1) |
6.-[-(-3)]化简后是( )
| A. | -3 | B. | 3 | C. | ±3 | D. | 以上都不对 |
3.比-2大3的数是( )
| A. | 1 | B. | -1 | C. | -5 | D. | -6 |
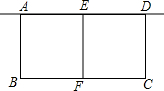 如图是一个矩形养鸡场的平面图,养鸡场由一堵旧墙(旧墙的长度不小于l米)和总长为l0米的篱笆围成,中间用篱笆分隔成两个小矩形.设大矩形的垂直于旧墙的一边长为x米,面积为s平方米.求s关于x的函数解析式,并写出这个函数的定义域.
如图是一个矩形养鸡场的平面图,养鸡场由一堵旧墙(旧墙的长度不小于l米)和总长为l0米的篱笆围成,中间用篱笆分隔成两个小矩形.设大矩形的垂直于旧墙的一边长为x米,面积为s平方米.求s关于x的函数解析式,并写出这个函数的定义域.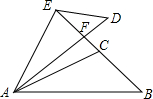 如图所示,△ABC≌△ADE,BC的延长线过点E,∠ACB=∠AED=105°,∠CAD=10°,∠B=50°,∠DEF的度数是35°.
如图所示,△ABC≌△ADE,BC的延长线过点E,∠ACB=∠AED=105°,∠CAD=10°,∠B=50°,∠DEF的度数是35°.