题目内容
11.某中学为丰富学生的校园生活,准备从某体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),商店推出了以下两种促销方案:
(1)购买一个足球、一个篮球各需多少元?
(2)根据该中学的实际情况,需从该体育用品商店一次性购买足球和篮球共80个.要求购买足球和篮球的总费用不超过5160元,这所中学想购买足够多的足球,求此时最佳的购买方案以及所用的钱数.
分析 (1)设每个篮球x元,每个足球y元,根据买2个篮球和3个足球共需368元,购买5个篮球和2个足球共需425元,列出方程组,求解即可;
(2)设买m个篮球,则购买(80-m)个足球,根据总价钱不超过5160元,列不等式求出x的最大整数解即可.
解答 解:(1)设每个篮球x元,每个足球y元,
由题意得,$\left\{\begin{array}{l}{2x+3y=368}\\{5x+2y=425}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=49}\\{y=90}\end{array}\right.$,
答:每个篮球49元,每个足球90元;
(2)设买m个篮球,则购买(80-m)个足球,
由题意得,49m+90(80-m)≤5160,
解得:m≤49$\frac{31}{41}$,
∵m为整数,
∴m最大取50,
则49×50+90(80-50)=5150(元)
答:最多可以买31个足球,需要的费用是5150元.
点评 本题考查了二元一次方程组的一元一次不等式的应用,解答本题的关键是读懂题意,找出合适的等量关系,列方程求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.我国最长的河流长江全长约6300千米,6300千米用科学记数法表示为( )
| A. | 6.3×102千米 | B. | 6.3×103千米 | C. | 0.63×104千米 | D. | 630×10千米 |
16.如果四个线段3,x,5,y的长度满足$\frac{3}{x}=\frac{5}{y}$,那么下列各式中不成立的一定是( )
| A. | $\frac{x}{y}=\frac{3}{5}$ | B. | $\frac{3+x}{x}=\frac{5+y}{y}$ | C. | $\frac{x}{y}=\frac{5}{3}$ | D. | $\frac{x-3}{3}=\frac{y-5}{5}$ |
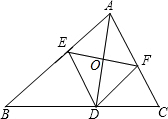 如图,在△ABC中,AD是△ABC的角平分线,DE∥AC,DF∥AB,EF交AD于点O,请问DO是△DEF的角平分线吗?请说明理由.
如图,在△ABC中,AD是△ABC的角平分线,DE∥AC,DF∥AB,EF交AD于点O,请问DO是△DEF的角平分线吗?请说明理由.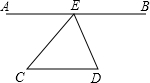 如图,已知点A,E,B在一同条直线上,设∠CED=x,∠C+∠D=y.
如图,已知点A,E,B在一同条直线上,设∠CED=x,∠C+∠D=y. 如图,直线AB与CD相交于点O,E是∠AOD内一点,已知OE⊥CD,∠AOE=40°,则∠BOD=50°.
如图,直线AB与CD相交于点O,E是∠AOD内一点,已知OE⊥CD,∠AOE=40°,则∠BOD=50°.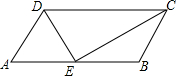 已知,如图,在平行四边形ABCD中,AB=2AD,E为AB的中点,连接DE,EC,求证:DE⊥EC.
已知,如图,在平行四边形ABCD中,AB=2AD,E为AB的中点,连接DE,EC,求证:DE⊥EC.