题目内容
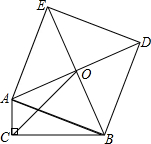 如图,Rt△ABC中,∠ACB=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC.
如图,Rt△ABC中,∠ACB=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC.(1)求证:CO平分∠ACB
(2)若AC=2,BC=4,求OC的长.
考点:正方形的性质,全等三角形的判定与性质,勾股定理
专题:
分析:(1)过点O作OM垂直于CA于点N,作ON垂直于CB于点N,易证四边形MCNO是矩形,利用已知条件再证明△AOM≌△BON,因为OM=ON,所以CO平分∠ACB;
(2)因为△AOM≌△BON,所以AM=BN,进而求出CN的长,根据勾股定理即可求出OC的长.
(2)因为△AOM≌△BON,所以AM=BN,进而求出CN的长,根据勾股定理即可求出OC的长.
解答:(1)证明:过点O作OM垂直于CA于点N,作ON垂直于CB于点N,
∴∠OMC=∠ONC=90°,
∵∠ACB=90°,
∴四边形MCNO是矩形,
∴∠MON=90°,
∵正方形 ABDE对角线交于点O,
∴OA=OB,∠AOB=90°,
∴∠MON-∠AON=∠AOB-∠AON,
∴∠AOM=∠NOB,
∵∠OMA=∠ONB=90°,
在△AOM和△BON中,
,
∴△AOM≌△BON(AAS),
∴OM=ON,
∴CO平分∠ACB
(2)解:∵△AOM≌△BON,
∴AM=BN,
∵AC=2,BC=4
∴CN=
=3,
∵∠OCN=45°,
∴ON=CN=3,
由勾股定理得OC=3
.
∴∠OMC=∠ONC=90°,
∵∠ACB=90°,

∴四边形MCNO是矩形,
∴∠MON=90°,
∵正方形 ABDE对角线交于点O,
∴OA=OB,∠AOB=90°,
∴∠MON-∠AON=∠AOB-∠AON,
∴∠AOM=∠NOB,
∵∠OMA=∠ONB=90°,
在△AOM和△BON中,
|
∴△AOM≌△BON(AAS),
∴OM=ON,
∴CO平分∠ACB
(2)解:∵△AOM≌△BON,
∴AM=BN,
∵AC=2,BC=4
∴CN=
| AC+BC |
| 2 |
∵∠OCN=45°,
∴ON=CN=3,
由勾股定理得OC=3
| 2 |
点评:本题考查了正方形的性质的运用,全等三角形的判定及性质的运用,勾股定理的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
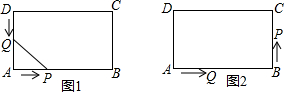 如图1,在长方形ABCD中,AB=12厘米,BC=6厘米.点P沿AB边从点A开始向点B以2厘米/秒的速度移动;点Q沿DA边从点D开始向点A以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间,那么:
如图1,在长方形ABCD中,AB=12厘米,BC=6厘米.点P沿AB边从点A开始向点B以2厘米/秒的速度移动;点Q沿DA边从点D开始向点A以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间,那么:
 “囧”(jiǒng)是近时期网络流行语,像一个人脸郁闷的神情.如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为x、y,剪去的两个小直角三角形的两直角边长也分别为x、y.
“囧”(jiǒng)是近时期网络流行语,像一个人脸郁闷的神情.如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为x、y,剪去的两个小直角三角形的两直角边长也分别为x、y. 如图,已知点E、C在线段BF上,BE=CF,请在下列四个等式中:①AB=DE,②∠ACB=∠F,③∠A=∠D,④AC=DF.选出两个作为条件,推出△ABC≌△DEF.并予以证明.(写出一种即可)
如图,已知点E、C在线段BF上,BE=CF,请在下列四个等式中:①AB=DE,②∠ACB=∠F,③∠A=∠D,④AC=DF.选出两个作为条件,推出△ABC≌△DEF.并予以证明.(写出一种即可)