题目内容
3. 如图,AH是⊙O的直径,AE平分∠FAH,交⊙O于点E,过点E的直线FG⊥AF,垂足为F,B为直径OH上一点,点E、F分别在矩形ABCD的边BC和CD上.
如图,AH是⊙O的直径,AE平分∠FAH,交⊙O于点E,过点E的直线FG⊥AF,垂足为F,B为直径OH上一点,点E、F分别在矩形ABCD的边BC和CD上.(1)求证:直线FG是⊙O的切线;
(2)若CD=8,EB=4,求⊙O的直径.
分析 (1)连结OE,如图,利用角平分线定义得到∠1=∠2,加上∠1=∠3,则∠2=∠3,于是可判断OE∥AF,则可利用AF⊥FG得到OE⊥FG,然后根据切线的判定定理得到直线FG是⊙O的切线;
(2)设⊙O的半径为r,则OA=OE=r,由矩形的性质得∠ABC=90°,AB=CD=8,然后在Rt△OBE中利用勾股定理得到(8-r)2+42=r2,解得r=5,于是得到⊙O的直径为10.
解答 (1)证明:连结OE,如图,
∵AE平分∠FAH,
∴∠1=∠2,
∵OA=OE,
∴∠1=∠3,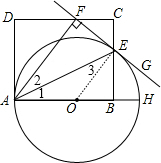
∴∠2=∠3,
∴OE∥AF,
∵AF⊥FG,
∴OE⊥FG,
∴直线FG是⊙O的切线;
(2)解:设⊙O的半径为r,则OA=OE=r,
∵四边形ABCD为矩形,
∴∠ABC=90°,AB=CD=8,
在Rt△OBE中,OB=8-r,BE=4,OE=r,
∴(8-r)2+42=r2,解得r=5,
∴⊙O的直径为10.
点评 本题考查了切线的判定:切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18. 如图,在平面直角坐标系中,点P的坐标为(0,2),直线y=$\frac{3}{4}x-3$与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为( )
如图,在平面直角坐标系中,点P的坐标为(0,2),直线y=$\frac{3}{4}x-3$与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为( )
 如图,在平面直角坐标系中,点P的坐标为(0,2),直线y=$\frac{3}{4}x-3$与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为( )
如图,在平面直角坐标系中,点P的坐标为(0,2),直线y=$\frac{3}{4}x-3$与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
8.某洗衣机厂原来库存洗衣机m台,现每天又生产n台存入库内,x天后该厂库存洗衣机的台数是( )
| A. | (m+nx)台 | B. | (mx+n)台 | C. | x(m+n)台 | D. | (mn+x)台 |
 如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AC=9,则CP的长为3.
如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AC=9,则CP的长为3. 如图,⊙O是△ABC的外接圆,BC是⊙O的直径,作∠CAD=∠B,且点D在BC延长线上.
如图,⊙O是△ABC的外接圆,BC是⊙O的直径,作∠CAD=∠B,且点D在BC延长线上. 如图,在△ABC中,BC=12cm,点M是∠ABC和∠ACB的角平分线的交点,且MD∥AB,ME∥AC,求△MDE的周长.
如图,在△ABC中,BC=12cm,点M是∠ABC和∠ACB的角平分线的交点,且MD∥AB,ME∥AC,求△MDE的周长.