题目内容
 如图1,在直角坐标系中,直线y=
如图1,在直角坐标系中,直线y=| 4 |
| 3 |
(1)A、B的坐标是A
(2)如图2,点D从O点出发沿x轴正方向以每秒1个单位的速度匀速前进;同时,点E从A出发在直线AB上沿AB方向以每秒2个单位的速度匀速前进.

①从出发开始,几秒后DE⊥AB?
②从出发开始,几秒后△ADE是等腰三角形?
考点:一次函数综合题
专题:动点型
分析:(1)分别令y=0和x=0解方程求解;
(2)设x秒后符合题意.则OD=x,AE=2x.
①当DE⊥AB时,根据△ADE∽△ABO列方程求解;
②分三种情况讨论求解:AD=AE;AE=DE;AD=DE.
(2)设x秒后符合题意.则OD=x,AE=2x.
①当DE⊥AB时,根据△ADE∽△ABO列方程求解;
②分三种情况讨论求解:AD=AE;AE=DE;AD=DE.
解答:解:(1)令y=0,得 x=-3.
∴A(-3,0);
令x=0,得 y=4.
∴B(0,4).
(2)在Rt△ABO中,AB=
=5.
设移动时间为x秒,则OD=x,AE=2x.

①如图1所示.当DE⊥AB时,有△ADE∽△ABO.
∴
=
,即
=
,
解得 x=
.
答:从出发开始,
秒后DE⊥AB;
②如图2所示,分三种情况:
Ⅰ.若AD=AE,则 2x=3+x.解得 x=3;
Ⅱ.若AE=DE,作EF⊥AD于点F.
则AF=
;△AEF∽△ABO.
∴
=
,即
=
.
解得 x=
;
Ⅲ.若AD=DE,作DC⊥AB于点C.
则AC=x;△ACD∽△AOB.
∴
=
,即
=
.
解得 x=
.
综上所述,从出发开始,3秒或
秒或
秒后△ADE是等腰三角形.
∴A(-3,0);
令x=0,得 y=4.
∴B(0,4).
(2)在Rt△ABO中,AB=
| 32+42 |
设移动时间为x秒,则OD=x,AE=2x.

①如图1所示.当DE⊥AB时,有△ADE∽△ABO.
∴
| AE |
| AO |
| AD |
| AB |
| 2x |
| 3 |
| x+3 |
| 5 |
解得 x=
| 9 |
| 7 |
答:从出发开始,
| 9 |
| 7 |
②如图2所示,分三种情况:
Ⅰ.若AD=AE,则 2x=3+x.解得 x=3;
Ⅱ.若AE=DE,作EF⊥AD于点F.
则AF=
| 3+x |
| 2 |
∴
| AF |
| AO |
| AE |
| AB |
| ||
| 3 |
| 2x |
| 5 |
解得 x=
| 15 |
| 7 |
Ⅲ.若AD=DE,作DC⊥AB于点C.
则AC=x;△ACD∽△AOB.
∴
| AC |
| AO |
| AD |
| AB |
| x |
| 3 |
| 3+x |
| 5 |
解得 x=
| 9 |
| 2 |
综上所述,从出发开始,3秒或
| 15 |
| 7 |
| 9 |
| 2 |
点评:此题考查了一次函数的综合应用,运用了分类讨论的数学思想和方法,结合相似三角形的判定和性质解答问题,综合性很强,难度较大.

练习册系列答案
相关题目
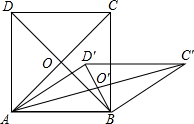 已知正方形ABCD的边长为1,O为其对角线交点,若保持AB不动,将正方形向顺时针方向压扁,得到菱形ABC′D′(如图).若∠BAD′=30°,则点O运动的路程为( )
已知正方形ABCD的边长为1,O为其对角线交点,若保持AB不动,将正方形向顺时针方向压扁,得到菱形ABC′D′(如图).若∠BAD′=30°,则点O运动的路程为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图为一个几何体的三视图,左视图和主视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的全面积为( )
如图为一个几何体的三视图,左视图和主视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的全面积为( )A、
| ||||
B、12
| ||||
| C、24 | ||||
D、24+2
|
 有一种皮球是由40块黑白相间的牛皮缝制而成的(如图),黑皮可看作五边形,白皮可看作六边形,每块黑皮的周围都是白皮,而每块白皮有三条边和黑皮边在一起,则白皮有( )
有一种皮球是由40块黑白相间的牛皮缝制而成的(如图),黑皮可看作五边形,白皮可看作六边形,每块黑皮的周围都是白皮,而每块白皮有三条边和黑皮边在一起,则白皮有( )| A、16块 | B、20块 |
| C、25块 | D、26块 |
已知一元二次方程x2+mx+3=0配方后为(x+n)2=22,那么一元二次方程x2-mx-3=0配方后为( )
| A、(x+5)2=28 |
| B、(x+5)2=19或(x-5)2=19 |
| C、(x-5)2=19 |
| D、(x+5)2=28或(x-5)2=28 |
若|2007-m|+
=m,则m-20072=( )
| m-2008 |
| A、2007 |
| B、2008 |
| C、20082 |
| D、-20082 |
 如图所示,正方形ABCD的面积设为1,E和F分别是AB和BC的中点,则图中阴影部分的面积是
如图所示,正方形ABCD的面积设为1,E和F分别是AB和BC的中点,则图中阴影部分的面积是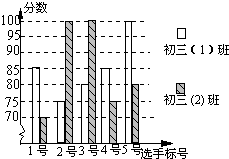 某中学开展“八荣八耻”演讲比赛活动,初三(1)班、(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示.
某中学开展“八荣八耻”演讲比赛活动,初三(1)班、(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示.