题目内容
11.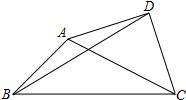 已知△ABC中,∠ABC=45°,AB=7$\sqrt{2}$,BC=17,以AC为斜边在△ABC外作等腰Rt△ACD,连接BD,则BD的长为$\frac{25\sqrt{2}}{2}$.
已知△ABC中,∠ABC=45°,AB=7$\sqrt{2}$,BC=17,以AC为斜边在△ABC外作等腰Rt△ACD,连接BD,则BD的长为$\frac{25\sqrt{2}}{2}$.
分析 显然直接求BD不好入手,那么就将问题进行转化.注意到△ACD为等腰Rt△,于是以AB为腰向左作等腰Rt△ABE,则易证△ABD与△AEC相似,相似比为$\frac{1}{\sqrt{2}}$,从而只需求出EC即可,此时∠EBC=135°,于是过E作EF⊥BC于F,则△EFB也为等腰Rt△,算出EF、BF,进而算出EC,问题迎刃而解.
解答 解:以AB为腰作等腰Rt△ABE,连接EC,
∵△ADC为等腰Rt△,
∴$\frac{AD}{AC}=\frac{1}{\sqrt{2}}=\frac{AB}{AE}$,∠EAB=∠DAC=45°,
∴∠EAB+∠BAC=∠BAC+∠DAC,
∴∠EAC=∠DAB,
∴△EAC∽△BAD,
∴$\frac{BD}{EC}=\frac{1}{\sqrt{2}}$,
作EF⊥BC交BC延长线于F,
∵∠ABC=45°,∠EBA=90°,
∴∠EBF=45°,
∴△EFB为等腰Rt△,
∴EF=FB=$\frac{\sqrt{2}}{2}EB$=$\frac{\sqrt{2}}{2}AB$=7,
∴EC=$\sqrt{E{F}^{2}+F{C}^{2}}$=25,
∴BD=$\frac{\sqrt{2}}{2}EC$=$\frac{25\sqrt{2}}{2}$.
点评 本题主要考查了等腰直角三角形的判定与性质、相似三角形的判定与性质、勾股定理等重要知识点,有一定难度.正确作出辅助线是本题的难点.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
20.绝对值大于2且不大于5的所有的整数的和是( )
| A. | 7 | B. | -7 | C. | 0 | D. | 5 |
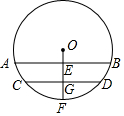 如图,圆柱形水管内原有积水的水平面宽CD=10cm,水深GF=1cm,若水面上升1cm(EG=1cm),则此时水面宽AB为多少?
如图,圆柱形水管内原有积水的水平面宽CD=10cm,水深GF=1cm,若水面上升1cm(EG=1cm),则此时水面宽AB为多少?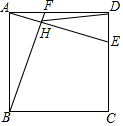 如图,在边长为2的正方形ABCD中,点E在边DC上运动,点F在边AD上运动,且DE=AF,AE,BF交于点H,连接DH,则DH的最小值为$\sqrt{5}-1$.
如图,在边长为2的正方形ABCD中,点E在边DC上运动,点F在边AD上运动,且DE=AF,AE,BF交于点H,连接DH,则DH的最小值为$\sqrt{5}-1$.
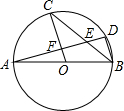 如图,AB是圆O的直径,C、D是圆O上的点,且OC∥BD,AD分别与BC、OC相交于点E、F.则下列结论:
如图,AB是圆O的直径,C、D是圆O上的点,且OC∥BD,AD分别与BC、OC相交于点E、F.则下列结论: