题目内容
1.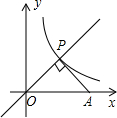 如图,点P是正比例函数y=x与反比例函数y=$\frac{k}{x}$在第一象限内的交点,PA⊥OP交x轴于点A,△POA的面积为2,则k的值是( )
如图,点P是正比例函数y=x与反比例函数y=$\frac{k}{x}$在第一象限内的交点,PA⊥OP交x轴于点A,△POA的面积为2,则k的值是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 P在y=x上可知△POA为等腰直角三角形,过P作PC⊥OA于点C,则可知S△POC=S△PCA=$\frac{1}{2}$k,可求得k的值.
解答 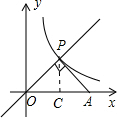 解:过P作PC⊥OA于点C,
解:过P作PC⊥OA于点C,
∵P点在y=x上,
∴∠POA=45°,
∴△POA为等腰直角三角形,
过P作PC⊥OA于C,
则S△POC=S△PCA=$\frac{1}{2}$k,
∴S△POA=k=2,
故选A.
点评 本题考查了反比例函数y=$\frac{k}{x}$(k≠0)系数k的几何意义:从反比例函数y=$\frac{k}{x}$(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.也考查了等腰直角三角形的性质.

练习册系列答案
相关题目
9.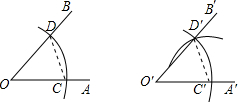 请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,要说明∠D′O′C′=∠DOC,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是( )
请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,要说明∠D′O′C′=∠DOC,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是( )
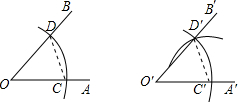 请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,要说明∠D′O′C′=∠DOC,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是( )
请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,要说明∠D′O′C′=∠DOC,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是( )| A. | 边边边 | B. | 边角边 | C. | 角边角 | D. | 角角边 |
16.计算a3•($\frac{1}{a}$)2的结果是( )
| A. | a | B. | a5 | C. | a6 | D. | a8 |
13. 如图,直线y=-x+m与y=x+3的交点的横坐标为-2,则关于x的不等式-x+m>x+3>0的取值范围为( )
如图,直线y=-x+m与y=x+3的交点的横坐标为-2,则关于x的不等式-x+m>x+3>0的取值范围为( )
 如图,直线y=-x+m与y=x+3的交点的横坐标为-2,则关于x的不等式-x+m>x+3>0的取值范围为( )
如图,直线y=-x+m与y=x+3的交点的横坐标为-2,则关于x的不等式-x+m>x+3>0的取值范围为( )| A. | x>-2 | B. | x<-2 | C. | -3<x<-2 | D. | -3<x<-1 |
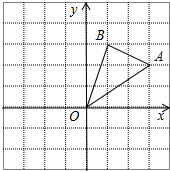 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O逆时针旋转90°后得到△A1OB1.
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O逆时针旋转90°后得到△A1OB1. 如图,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动.设∠APB=y(单位:度),那么y关于点P运动的时间x(单位:秒)的函数图象大致是( )
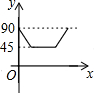
如图,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动.设∠APB=y(单位:度),那么y关于点P运动的时间x(单位:秒)的函数图象大致是( )


 如图,△ABC中,AB=AC,AB的垂直平分线交边AB于D点,交边AC于E点,若△ABC与△EBC的周长分别是40cm,24cm,则AB=16cm.
如图,△ABC中,AB=AC,AB的垂直平分线交边AB于D点,交边AC于E点,若△ABC与△EBC的周长分别是40cm,24cm,则AB=16cm.