题目内容

11．如图，△ABC中，AB=AC，AB的垂直平分线交边AB于D点，交边AC于E点，若△ABC与△EBC的周长分别是40cm，24cm，则AB=16cm．

分析 首先根据DE是AB的垂直平分线，可得AE=BE；然后根据△ABC的周长=AB+AC+BC，△EBC的周长=BE+EC+BC=AE+EC+BC=AC+BC，可得△ABC的周长-△EBC的周长=AB，据此求出AB的长度是多少即可．

解答 解：∵DE是AB的垂直平分线，
∴AE=BE；
∵△ABC的周长=AB+AC+BC，△EBC的周长=BE+EC+BC=AE+EC+BC=AC+BC，
∴△ABC的周长-△EBC的周长=AB，
∴AB=40-24=16（cm）．
故答案为：16．

点评 （1）此题主要考查了垂直平分线的性质，要熟练掌握，解答此题的关键是要明确：垂直平分线上任意一点，到线段两端点的距离相等．
（2）此题还考查了等腰三角形的性质，以及三角形的周长的求法，要熟练掌握．

练习册系列答案
相关题目
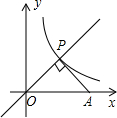1．如图，点P是正比例函数y=x与反比例函数y=$\frac{k}{x}$在第一象限内的交点，PA⊥OP交x轴于点A，△POA的面积为2，则k的值是（　　）
A．2B．3C．4D．5
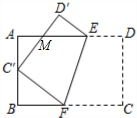2．如图，将矩形ABCD沿EF折叠，使顶点C恰好落在AB边的中点C′上，点D落在D′处，C′D′交AE于点M．若AB=6，BC=9，则AM的长为$\frac{9}{4}$．
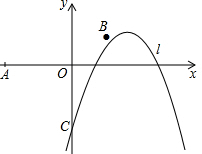19．如图，已知点O（0，0），A（-5，0），B（2，1），抛物线l：y=-（x-h）2+1（h为常数）与y轴的交点为C．
（1）l经过点B，求它的解析式，并写出此时l的对称轴及顶点坐标；
（2）设点C的纵坐标为yc，求yc的最大值，此时l上有两点（x1，y1），（x2，y2），其中x1＞x2≥0，比较y1与y2的大小；
（3）当线段OA被l只分为两部分，且这两部分的比是1：4时，求h的值．
6．已知四边形ABCD内接于⊙O，∠ADC=90°，∠DCB＜90°，对角线AC平分∠DCB，延长DA，CB相交于点E．
（1）如图1，EB=AD，求证：△ABE是等腰直角三角形；
（2）如图2，连接OE，过点E作直线EF，使得∠OEF=30°，当∠ACE≥30°时，判断直线EF与⊙O的位置关系，并说明理由．
16．如图是一个正方体纸盒的展开图，其中的六个正方形内分别标有数字“0”、“1”、“2”、“5”和汉字、“数”、“学”，将其围成一个正方体后，则与“5”相对的是（　　）
A．0B．2C．数D．学
3．下列计算正确的是（　　）
A．$\sqrt{12}$-$\sqrt{3}$=$\sqrt{3}$B．a6÷a3=a2C．（a+b）2=a2+b2D．2a+3b=5ab
20．如图，在△ABC中，AB=AC，DE∥BC，则下列结论中不正确的是（　　）
A．AD=AEB．DB=ECC．∠ADE=∠CD．DE=$\frac{1}{2}$BC
7．不等式组$\left\{\begin{array}{l}{2x-1＜5}\\{x-2＞-3}\end{array}\right.$的解集是（　　）
A．1＜x＜6B．-1＜x＜3C．1＜x＜3D．-1＜x＜6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网