题目内容
17.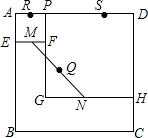 如图,四边形ABCD是边长为8的正方形,点R、S在边AD上,且AR=1,SD=2,点P是线段RS上的动点,分别以AP、PD为边在正方形ABCD内作正方形AEFP和PGHD,M、N分别为EF、GH的中点.连结MN,设MN的中点为0,则当点P从点R运动到点S时,点O移动的路径长为2.5.
如图,四边形ABCD是边长为8的正方形,点R、S在边AD上,且AR=1,SD=2,点P是线段RS上的动点,分别以AP、PD为边在正方形ABCD内作正方形AEFP和PGHD,M、N分别为EF、GH的中点.连结MN,设MN的中点为0,则当点P从点R运动到点S时,点O移动的路径长为2.5.
分析 设BC中点为K,连接PM、MK、KN、PN、PK,可证明四边形PMKN为平行四边形,判断出Q的运行轨迹为△KSR的中位线,从而求出点Q移动的路径长.
解答 解:设BC中点为K,连接PM、MK、KN、PN、PK,
∵E为MN的中点,S为KH的中点
∴A,M,K共线,
N为GH的中点,K为BC的中点,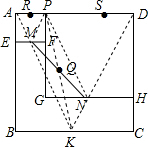
∴SNK共线,
由△AEM∽△PGN,得∠KAP=∠NPD,
∴MK∥PN,
由△PFM∽△DRN,得∠MPA=∠NDP,
∴PM∥NK,
则四边形PMKN为平行四边形,则Q为PK的中点,
∴Q的轨迹为△RKS的中位线,
∵CD=AD-AR-SD=8-1-2=5,
∴点Q移动的路径为$\frac{1}{2}$×5=2.5.
故答案为:2.5.
点评 本题考查了轨迹,判断出Q的运行轨迹为△RKS的中位线是解题的关键.

练习册系列答案
相关题目
8.今年某初中有近1千名考生参加中考,为了了解这些考生的数学成绩,从中抽取50名考生的数学成绩进行统计分析,以下说法正确的是( )
| A. | 这50名考生是总体的一个样本 | B. | 近1千名考生是总体 | ||
| C. | 每位考生的数学成绩是个体 | D. | 50名学生是样本容量 |
6.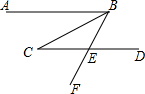 如图,已知AB∥CD,BC平分∠ABE,∠C=33°,则∠CEF的度数是( )
如图,已知AB∥CD,BC平分∠ABE,∠C=33°,则∠CEF的度数是( )
 如图,已知AB∥CD,BC平分∠ABE,∠C=33°,则∠CEF的度数是( )
如图,已知AB∥CD,BC平分∠ABE,∠C=33°,则∠CEF的度数是( )| A. | 16° | B. | 33° | C. | 49° | D. | 66° |
7.-3的绝对值是( )
| A. | 3 | B. | -$\frac{1}{3}$ | C. | -3 | D. | $\frac{1}{3}$ |
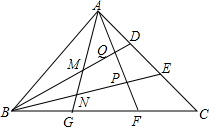 △ABC面积为S,AD=DE=EC,BG=GF=FC,AG,AF与BD,BE分别交于M,N,P,Q,连接EF.
△ABC面积为S,AD=DE=EC,BG=GF=FC,AG,AF与BD,BE分别交于M,N,P,Q,连接EF.