题目内容
19.函数直线y=2x-3的图象与x轴交点坐标为($\frac{3}{2}$,0),与y轴的交点坐标为(0,-3),与两坐标轴围成的三角形面积是$\frac{9}{4}$.分析 根据x轴上点的坐标特征计算函数值为0时的自变量的值即可得到直线与x轴交点坐标,然后根据三角形面积公式计算直线与两坐标轴围成的三角形面积.
解答 解:当y=0时,2x-3=0,解得x=$\frac{3}{2}$,则直线与x轴交点坐标为($\frac{3}{2}$,0),
所以直线与两坐标轴围成的三角形面积=$\frac{1}{2}$×$\frac{3}{2}$×3=$\frac{9}{4}$.
故答案为($\frac{3}{2}$,0),$\frac{9}{4}$.
点评 本题考查了一次函数图象上点的坐标特征:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-$\frac{b}{k}$,0);与y轴的交点坐标是(0,b).直线上任意一点的坐标都满足函数关系式y=kx+b.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.小明的爸爸骑着摩托车带着小明在公路上匀速行驶,小明每隔一段时间看到的里程碑上的数如下:时刻12:0013:0014:30碑上的数是一个两位数,数字之和为6十位与个位数字与12:00时所看到的正好颠倒了比12:00时看到的两位数中间多了个0则12:00时看到的两位数是( )
| 时刻 | 12:00 | 13:00 | 14:30 |
| 碑上 的数 | 是一个两位数,数字之和为6 | 十位与个位数字与12:00时所看到的正好颠倒了 | 比12:00时看到的两位数中间多了个0 |
| A. | 24 | B. | 42 | C. | 51 | D. | 15 |
11.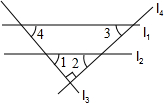 如图,直线l1∥l2,l3⊥l4,有下列三个命题,①∠1+∠3=90°;②∠2+∠3=90°;③∠2=∠4,则( )
如图,直线l1∥l2,l3⊥l4,有下列三个命题,①∠1+∠3=90°;②∠2+∠3=90°;③∠2=∠4,则( )
 如图,直线l1∥l2,l3⊥l4,有下列三个命题,①∠1+∠3=90°;②∠2+∠3=90°;③∠2=∠4,则( )
如图,直线l1∥l2,l3⊥l4,有下列三个命题,①∠1+∠3=90°;②∠2+∠3=90°;③∠2=∠4,则( )| A. | 只有①正确 | B. | 只有②正确 | C. | ①和③正确 | D. | ①②③都正确 |
8. 如图所示,图中的三个矩形中相似的是( )
如图所示,图中的三个矩形中相似的是( )
 如图所示,图中的三个矩形中相似的是( )
如图所示,图中的三个矩形中相似的是( )| A. | 甲、乙和丙 | B. | 甲和乙 | C. | 甲和丙 | D. | 乙和丙 |
9.设圆锥侧面展开图的圆心角为n°,母线长为R,底面半径为r.填表:
| n | 60° | 72° | 90° | 120° |
| R关于r的函数解析式 | 6r | 5r | 4r | 3r |




 如图,是用硬纸板做成的两个小直角三角形和一个大直角三角形,两个小直角三角形直角边长分别为a和b,斜边为c,大直角三角形直角边都为c,请你动动脑筋,将它们拼成一个能证明勾股定理的图形,并用这个图形证明勾股定理.
如图,是用硬纸板做成的两个小直角三角形和一个大直角三角形,两个小直角三角形直角边长分别为a和b,斜边为c,大直角三角形直角边都为c,请你动动脑筋,将它们拼成一个能证明勾股定理的图形,并用这个图形证明勾股定理.