题目内容
7. 如图,是用硬纸板做成的两个小直角三角形和一个大直角三角形,两个小直角三角形直角边长分别为a和b,斜边为c,大直角三角形直角边都为c,请你动动脑筋,将它们拼成一个能证明勾股定理的图形,并用这个图形证明勾股定理.
如图,是用硬纸板做成的两个小直角三角形和一个大直角三角形,两个小直角三角形直角边长分别为a和b,斜边为c,大直角三角形直角边都为c,请你动动脑筋,将它们拼成一个能证明勾股定理的图形,并用这个图形证明勾股定理.
分析 根据图形可知是梯形,再根据梯形的面积等于三个直角三角形的面积的和,列式整理即可证明.
解答 解:如图所示,这是一个梯形.
证明:∵S梯形ABCD=S△ABE+S△AED+S△ECD,
∴$\frac{1}{2}$(a+b)•(a+b)=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$ab,
∴(a+b)2=ab+c2+ab,a2+2ab+b2=2ab+c2,
∴a2+b2=c2.
点评 本题考查了勾股定理的证明,根据图形的面积列式整理即可,题中图形答案不唯一,富有创造性,只要是根据面积可以推出勾股定理即可.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
15.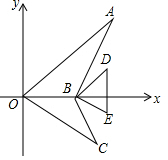 如图,将平面直角坐标系中图案的六个点的纵坐标保持不变,横坐标分别变成原来的2倍,连接各点所得图案与原图案相比( )
如图,将平面直角坐标系中图案的六个点的纵坐标保持不变,横坐标分别变成原来的2倍,连接各点所得图案与原图案相比( )
 如图,将平面直角坐标系中图案的六个点的纵坐标保持不变,横坐标分别变成原来的2倍,连接各点所得图案与原图案相比( )
如图,将平面直角坐标系中图案的六个点的纵坐标保持不变,横坐标分别变成原来的2倍,连接各点所得图案与原图案相比( )| A. | 相同 | B. | 横向缩短一半 | C. | 横向拉长2倍 | D. | 纵向拉长2倍 |
16.王明同学随机抽查某市10个小区所得到的绿化率情况,结果如下表:
则关于这10个小区的绿化率情况,下列说法错误的是( )
| 小区绿化率(%) | 20 | 25 | 30 | 32 |
| 小区个数 | 2 | 4 | 3 | 1 |
| A. | 方差是13% | B. | 众数是25% | C. | 中位数是25% | D. | 平均数是26.2% |
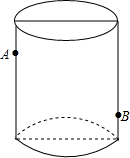 如图,有一个圆柱形杯子,底面周长为12cm,高为8cm,A点在内壁距杯口2cm处,在A点正对面的外壁距杯底2cm的B处有一只小虫,小虫要到A处饱餐一顿至少要走10cm.(杯子厚度忽略不计)
如图,有一个圆柱形杯子,底面周长为12cm,高为8cm,A点在内壁距杯口2cm处,在A点正对面的外壁距杯底2cm的B处有一只小虫,小虫要到A处饱餐一顿至少要走10cm.(杯子厚度忽略不计)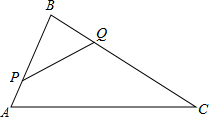 如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB向B以2cm/s的速度移动,点Q从点B开始沿BC向C点以4cm/s的速度移动.如果P,Q分别从A,B同时出发,经过几秒钟△PBQ与△ABC相似?
如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB向B以2cm/s的速度移动,点Q从点B开始沿BC向C点以4cm/s的速度移动.如果P,Q分别从A,B同时出发,经过几秒钟△PBQ与△ABC相似?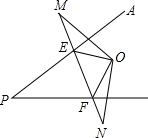 如图所示,已知O是∠APB内的一点,点M、N分别是O点关于PA、PB的对称点,MN与PA、PB分别相交于点E、F,已知MN=5cm.
如图所示,已知O是∠APB内的一点,点M、N分别是O点关于PA、PB的对称点,MN与PA、PB分别相交于点E、F,已知MN=5cm.