题目内容
如图1,在平面直角坐标系中,开口向上的抛物线与 轴交于
轴交于 两点,
两点,  为抛物线的顶点,
为抛物线的顶点,  为坐标原点,过点
为坐标原点,过点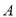 作
作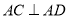 交抛物线于点
交抛物线于点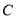 . 若
. 若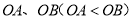 的长分别是方程
的长分别是方程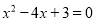 的两根,且
的两根,且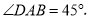
(1)求抛物线对应的二次函数解析式和点 的坐标。
的坐标。
(2)若点M为x轴正半轴上一个动点,N为线段AC上的一个动点,连接MN、CM,是否存在这样的点M,使△AMN为直角三角形和△CMN为等腰三角形同时成立,如果存在,请求出所有符合条件的点M的坐标,如果不存在,请说明理由。
(3如图2,过点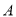 任作直线
任作直线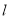 交线段
交线段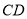 于点
于点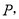 求
求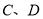 到直线
到直线 的距离分别为
的距离分别为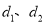 ,请直接写出
,请直接写出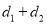 的最大值.
的最大值.

图1 图2
练习册系列答案
相关题目
在对第一章“丰富的图形世界”复习前,老师让学生整理正方体截面的形状并探究多面体(由若干个多边形所围成的几何体)的棱数、面数、顶点数之间的数量关系,如图是小颖用平面截正方体后剩余的多面体,请解答下列问题:
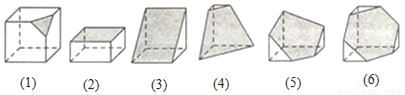
(1)根据上图完成下表:
多面体 | V(顶点数) | F(面数) | E(棱数) |
(1) |
| 7 | 15 |
(3) | 6 |
| 9 |
(5) | 8 | 6 |
|
(2)猜想:一个多面体的V(顶点数),F(面数),E(棱数)之间的数量关系是 ;
(3)计算:已知一个多面体有20个面、30条棱,那么这个多面体有 个顶点.

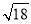 tan30°+(
tan30°+(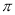 +4)0-|-
+4)0-|-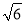 |
|

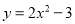 的图象是一条抛物线,下列关于该抛物线的说法正确的是( )
的图象是一条抛物线,下列关于该抛物线的说法正确的是( )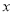 轴有两个交点
轴有两个交点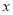 =1 D. 抛物线经过点(2,3)
=1 D. 抛物线经过点(2,3)