题目内容
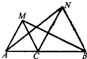如图，C在线段AB上，在AB的同侧作等边三角形△ACM和△BCN，连接AN，BM，若∠MBN=38°，则∠ANB=82°
82°
．分析：根据等边三角形的边相等，角相等，能证明△ACN和△MCB全等，则∠ANC和∠MBA相等，∠MBA=60°-∠MBN=60°-38°=22°，所以可求出∠ANB的解．
解答：解：∵△ACM和△BCN是等边三角形，
∴AC=MC，CB=CN，∠ACM+∠MCN=∠BCN+∠MCN，
即∠ACN=∠MCB．
∴△ACN≌△MCB．
∴∠ANC=∠MBA．
∵∠MBA=60°-∠MBN=60°-38°=22°，
∴∠ANC=22°．
∴∠ANB=22°+60°=82°．
故答案为：82°．
∴AC=MC，CB=CN，∠ACM+∠MCN=∠BCN+∠MCN，
即∠ACN=∠MCB．
∴△ACN≌△MCB．
∴∠ANC=∠MBA．
∵∠MBA=60°-∠MBN=60°-38°=22°，
∴∠ANC=22°．
∴∠ANB=22°+60°=82°．
故答案为：82°．
点评：本题考查等边三角形的性质以及全等三角形的判定和性质，本题关键知道∠ACN和∠MCB相等．
练习册系列答案
相关题目
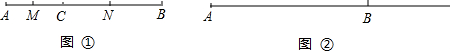
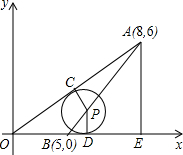如图点P在线段AB上，⊙P与x轴相切于D点，且与线段AO相切于C点，已知A、B两点的坐标分别是（8，6），（5，0），
如图点C在线段AB上，AC=2BC，M、N分别为AC、BC的中点，若BC=4cm，求线段MN的长．