题目内容
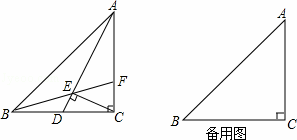
如图,已知Rt△ABC中,∠ACB=90°,AC=BC,D为CB边上一动点,CD= BC,连接AD,CE⊥AD于点E,延长线BE交AC于点F.
BC,连接AD,CE⊥AD于点E,延长线BE交AC于点F.
(1)若n=3,则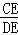 = ,
= ,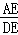 = ;
= ;
(2)若n=2,求证:AF=2FC;
(3)若F为AC的中点,请直接写出n的值.
考点: 相似三角形的判定与性质.
分析: (1)通过证明△CED∽△ACD,根据相似比即可求得CE:DE的长,同理可求得AE:DE的值.
(2)根据已知可求得△GED∽△AFE,根据相似比即可求得AF,FC的关系.
(3)要使AF=CF,必需n2=(n﹣1):n.
解答: 解:(1)由题意得,∠DEC=∠DCA=90°,∠EDC=∠CDA,
∴△CED∽△ACD.
∴CE:DE=AC:CD.
∵AC=BC,
∴AC:CD=n=3.
∴CE:DE=3.
同理可得:AE:DE=9.
故答案为:3,9.
(2)如图,当n=2时,D为BC的中点,取BF的中点G,连接DG,
则DG= FC,DG∥FC.
FC,DG∥FC.
∵CE⊥AD,∠ACB=90°,
∴∠ECD+∠EDC=∠CAD+∠ADC=90°.
∴∠ECD=∠CAD.
∵tan∠ECD=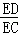 ,tan∠CAD=
,tan∠CAD=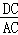 =
=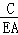 ,
,
∴ =
=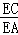 =
= .
.
∵AC=BC,BC=2DC,
∴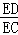 =
=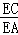 =
= =
= .
.
∴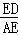 =
=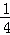 .
.
∵DG∥FA,
∴△GDE∽△FAE.
∴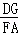 =
=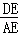 .
.
∴DG=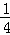 AF.
AF.
∵DG= FC,
FC,
∴AF=2FC.
(3)如图,∵BC=nDC,
∴DC:BC=1:n,
∴DC:AC=1:n,
∴DE:CE:AE=1:n:n2;
∴DG:AF=1:n2;
又∵DG:CF=DB:BC=(BC﹣CD):BC=(n﹣1):n
要使AF=CF,必需n2=n:(n﹣1),(n>0)
∴当n=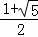 ,F为AC的中点.
,F为AC的中点.

点评: 本题主要考查了相似三角形的判定与性质,关键是根据相似三角形得出线段之间的比例关系,进而得出所求线段与n之间的关系.

 (其中
(其中 、
、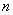 均为非零常数),这里等式右边是通常的四则运算,例如:
均为非零常数),这里等式右边是通常的四则运算,例如: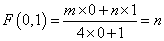 .
.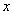 的不等式组
的不等式组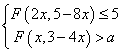 有解,求实数
有解,求实数 的取值范围;
的取值范围;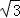 .⊙P运动一圈与△OBC的边相切 次,每次相切时,点P到等边三角形顶点最近距离是 .
.⊙P运动一圈与△OBC的边相切 次,每次相切时,点P到等边三角形顶点最近距离是 .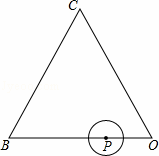
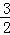 B. x<3 C. x>
B. x<3 C. x>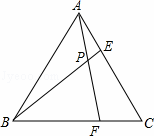
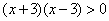 .
.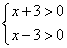 或(2)
或(2) 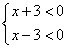
 .
. .
.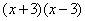 的解集为
的解集为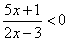 的解集.
的解集.