题目内容
20.(1)计算($\sqrt{48}$-$\sqrt{75}$)×$\sqrt{1\frac{1}{3}}$(2)解方程:$\frac{3-x}{x-4}$+$\frac{1}{4-x}$=1.
分析 (1)按照乘法的分配律进行计算,然后再开方即可;
(2)先去分母,将分式方程转化为整式方程,然后再解这个整式方程,最后再进行检验即可.
解答 解:(1)原式=$\sqrt{48}×\sqrt{1\frac{1}{3}}$-$\sqrt{75}×\sqrt{1\frac{1}{3}}$
=$\sqrt{64}-\sqrt{100}$
=8-10
=-2
(2)方程两边同时乘以x-4得:3-x-1=x-4
解得:x=3
将x=3代入最简公分母x-4=3-4=-1≠0,
∴x=3是原方程的解.
点评 本题主要考查的是二次根式的混合运算和解分式方程,掌握利用乘法的分配律进行简便运算以及掌握分式方程的解法是解题的关键.

练习册系列答案
相关题目
10.某校举办“汉字听写”大赛15名学生进入决赛,他们所得分数互不相同,比赛共设8个获奖名额,某学生知道自己的分数后,要判断自己能否获奖,他应该关注的统计量是( )
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
15.下列各式中,与$\sqrt{3}$是同类二次根式的是( )
| A. | $\sqrt{6}$ | B. | $\sqrt{15}$ | C. | $\sqrt{18}$ | D. | $\sqrt{\frac{1}{12}}$ |
10.已知点P(x.y)在x轴上方,且|x|=2,|y|=3,则点P的坐标是( )
| A. | (2,3) | B. | (-2,3) | C. | (2,-3) | D. | (2,3)或(-2,3) |
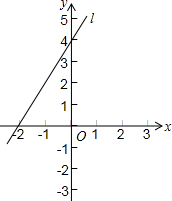 如图所示,直线l是一次函数的图象
如图所示,直线l是一次函数的图象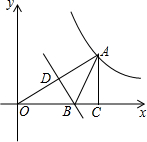 如图,点A在双曲线y=$\frac{3}{x}$(x>0)上,过点A作AC⊥x轴,垂足为C,线段OA的垂直平分线BD交x轴于点B,△ABC的周长为4,求点A的坐标.
如图,点A在双曲线y=$\frac{3}{x}$(x>0)上,过点A作AC⊥x轴,垂足为C,线段OA的垂直平分线BD交x轴于点B,△ABC的周长为4,求点A的坐标.