题目内容
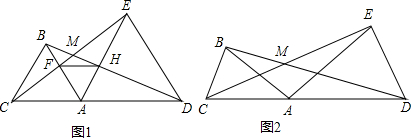
19.如图,点A是线段CD上一点,且AC<AD.(1)如图1,当△ABC和△AED都是等边三角形时,连接CE,BD,分别交AB、AE于点F、H.
①求证:BD=CE;
②求:∠BMC的度数;
③判断△AFH是何特殊三角形并说明理由;
(2)如图2,当AB=AC,AD=AE,∠ABC=∠ADE=a时,直接写出BD与CE的数量关系和∠BMC的度数(用a表示).
分析 (1)①利用等边三角形的性质得到相等的边与角,证明△CAE≌△BAD(SAS)即可得到BD=CE.
②由①△CAE≌△BAD得∠BDA=∠CEA,根据∠BMC=∠MCD+∠CEA=180°-∠CAE,即可解答;
③证明△CAF≌△BAH(ASA),得到AF=AH,又∠FAH=60°,所以△AFH是等边三角形.
(2)首先根据已知得出∠BAD=∠CAE,进而得出△ABD≌△ACE,求出即可;利用△ABD≌△ACE,得出∠BDA=∠CEA,则∠BMC=∠MCD+∠CEA=∠EAD即可得出答案;
解答 (1)①证明:∵△ABC和△AED都是等边三角形
∴AC=AB,AE=AD,∠CAB=∠EAD=60°,
∴∠FAH=180°-60°-60°=60°
∴∠CAE=60°+60°=120°
∠BAD=60°+60°=120°
∴∠CAE=∠BAD,
在△CAE和△BAD中,
$\left\{\begin{array}{l}{AC=AB}\\{∠CAE=∠BAD}\\{AE=AD}\end{array}\right.$
∴△CAE≌△BAD(SAS)
∴BD=CE.
②∵∠BMC=∠MCD+∠BDA,
由①△CAE≌△BAD得∠BDA=∠CEA、
∴∠BMC=∠MCD+∠CEA=180°-∠CAE=180°-120°=60°.
③△AFH是等边三角形,
理由:由①△CAE≌△BAD得∠ACF=∠ABH,
在△CAF和△BAH中,
$\left\{\begin{array}{l}{∠ACF=∠ABH}\\{AC=AB}\\{∠CAF=∠BAH}\end{array}\right.$
∴△CAF≌△BAH(ASA)
∴AF=AH,
又∠FAH=60°,
∴△AFH是等边三角形.
(2)BD=CE,∠BMC=180°-2a;
理由:∵AD=AE,
∴∠AED=∠ADE=α,
∴∠DAE=180°-2∠ADE=180°-2α,
同理可得出:∠BAC=180°-2α,
∴∠DAE=∠BAC,
∴∠DAE+∠BAE=∠BAC+∠BAE,
即∠BAD=∠CAE,
在△ABD和△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△ABD≌△ACE(SAS),
∴BD=CE;
∵△ABD≌△ACE,
∴∠BDA=∠CEA,
∵∠BMC=∠MCD+∠MDC,
∴∠BMC=∠MCD+∠CEA=∠EAD=180°-2α.
点评 此题主要考查了相似三角形的判定与性质以及全等三角形的判定与性质等知识,根据已知得出∠BMC=∠MCD+∠CEA是解题关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | (x-4)2=2 | B. | (x-2)2=6 | C. | (x-2)2=8 | D. | (x-2)2=10 |
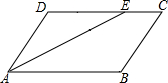 如图,在平行四边形ABCD中,∠BAD的平分线AE交边CD于点E,AB=6cm,BC=4cm,则EC=2cm.
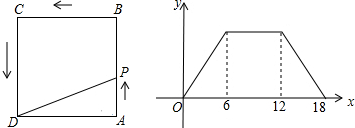
如图,在平行四边形ABCD中,∠BAD的平分线AE交边CD于点E,AB=6cm,BC=4cm,则EC=2cm. 如下图所示,将长方形ABCD的一角折起来,使得B点和E点重合,而通过E点可以将AD边3等分.求FG的长度.
如下图所示,将长方形ABCD的一角折起来,使得B点和E点重合,而通过E点可以将AD边3等分.求FG的长度.
 如图,在直角坐标系中,已知点A(0,2),点B(-2,0),过点B和线段OA的中点C作直线BC,以线段BC为边向上作正方形BCDE.
如图,在直角坐标系中,已知点A(0,2),点B(-2,0),过点B和线段OA的中点C作直线BC,以线段BC为边向上作正方形BCDE.