题目内容
如图,已知双曲线y=
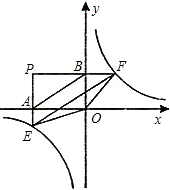
(k为常数)与过原点的直线相交于A、B两点,第一象限内的点M(点M在A的上方)是双曲线y=
上的一动点,设直线AM、BM分别与y轴交于P、Q两点.
(1)若直线AB的解析式为y=
x,A点的坐标为(a,1),
①求a、k的值;
②当AM=2MP时,求点P的坐标.
(2)若AM=m•MP,BM=n•MQ,试问m-n的值是否为定值?若是求出它的值;若不是,请说明理由.
| k-3 |
| x |
| k-3 |
| x |
(1)若直线AB的解析式为y=
| 1 |
| 6 |
①求a、k的值;
②当AM=2MP时,求点P的坐标.
(2)若AM=m•MP,BM=n•MQ,试问m-n的值是否为定值?若是求出它的值;若不是,请说明理由.

(1)①∵A(α,1)在直线 y=
x上,
∴
a=1,
解得a=6.
∵A(6,1)在双曲线 y=
上,
∴
=1,
解得k=9,
∴a,k 的值分别是6,9;
②如图1,过点A作AE⊥y轴于E,过点M作MF⊥y轴于F,
则MF∥AE,
∴△PMF∽△PAE,
∴
=
,即
=
,
∴MF=2,
∴点M(2,3).
∵A(6,1)、M(2,3),
∴直线AM的解析式为 y=-
x+4.
∴点P(0,4);
(2)答m-n=-2.
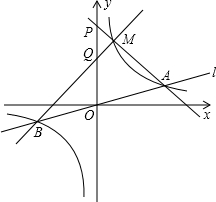
如图2,设点A的横坐标为b,点M的横坐标为t,则点B的横坐标为-b;
过点B作BC⊥y 轴于C,过点M作MD⊥AE于D.
∵MD∥y 轴,
∴△AMD∽△APE,
∴
=
,即
=
,得m=
①
∵MF∥BC,
∴△MFQ∽△BCQ,
∴
=
,即
=
,得n=
②
∴由①-②得,m-n=
-
=-2.

| 1 |
| 6 |
∴
| 1 |
| 6 |
解得a=6.
∵A(6,1)在双曲线 y=
| k-3 |
| x |
∴
| k-3 |
| x |
解得k=9,
∴a,k 的值分别是6,9;
②如图1,过点A作AE⊥y轴于E,过点M作MF⊥y轴于F,
则MF∥AE,
∴△PMF∽△PAE,
∴
| MF |
| AE |
| PM |
| PA |
| MF |
| 6 |
| 1 |
| 3 |
∴MF=2,
∴点M(2,3).
∵A(6,1)、M(2,3),
∴直线AM的解析式为 y=-
| 1 |
| 2 |
∴点P(0,4);
(2)答m-n=-2.
如图2,设点A的横坐标为b,点M的横坐标为t,则点B的横坐标为-b;
过点B作BC⊥y 轴于C,过点M作MD⊥AE于D.
∵MD∥y 轴,
∴△AMD∽△APE,
∴
| AM |
| AP |
| AD |
| AE |
| m |
| m+1 |
| b-t |
| b |
| b-t |
| t |
∵MF∥BC,
∴△MFQ∽△BCQ,
∴
| FM |
| BC |
| MQ |
| BQ |
| t |
| b |
| 1 |
| n-1 |
| b+t |
| t |
∴由①-②得,m-n=
| b-t |
| t |
| b+t |
| t |


练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目



 ,将△OAB绕O点顺时针旋转30°后,恰好A点在双曲线y=
,将△OAB绕O点顺时针旋转30°后,恰好A点在双曲线y=