题目内容
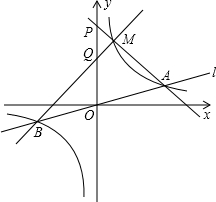
如图所示，边长为2的等边三角形OAB的顶点A在x轴的正半轴上，B点位于第一象限
，将△OAB绕O点顺时针旋转30°后，恰好A点在双曲线y=
（x＞0）上．
（1）求双曲线y=
（x＞0）的解析式；
（2）等边三角形OAB继续按顺时针方向旋转多少度后，A点再次落在双曲线上？
，将△OAB绕O点顺时针旋转30°后，恰好A点在双曲线y=| k |
| x |
（1）求双曲线y=
| k |
| x |
（2）等边三角形OAB继续按顺时针方向旋转多少度后，A点再次落在双曲线上？
（1）如图所示，
OA=2，∠AOD=30°，
在Rt△AOD中，
∴OD=OA•cos30°=2×
=
，
AD=OA•sin30°=2×
=1．
∴A（
，-1），
把x=
，y=-1代入y=
，
∴k=-
．
∴双曲线的解析式为y=-
（x＞0）；
（2）猜想等边三角形OAB继续按顺时针方向旋转30°后，A点再次落在双曲线上，
如图，此时A（1，-
），代入y=-
满足，
故猜想正确．
OA=2，∠AOD=30°，
在Rt△AOD中，
∴OD=OA•cos30°=2×
| ||
| 2 |
| 3 |
AD=OA•sin30°=2×
| 1 |
| 2 |
∴A（
| 3 |
把x=
| 3 |
| k |
| x |
∴k=-
| 3 |
∴双曲线的解析式为y=-
| ||
| x |
（2）猜想等边三角形OAB继续按顺时针方向旋转30°后，A点再次落在双曲线上，
如图，此时A（1，-
| 3 |
| ||
| x |
故猜想正确．
练习册系列答案
阅读快车系列答案
相关题目
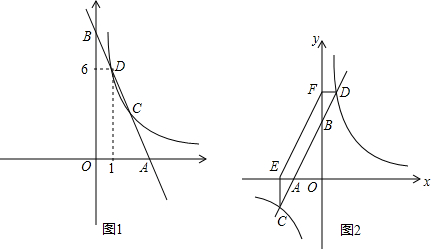
不变时，气球内气体的气压P（KPa）是气体体积V（m3）的反比例函数，其图象如图所示．
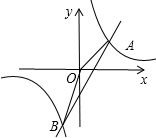
图象上，△P1OA1，△P2A1A2，△P3A2A3，…△PnAn-1An都是等腰直角三角形，斜边OA1、A1A2、A2A3，…An-1An都在x轴上