题目内容
已知：如图，EF⊥BC于点F，ED⊥AB于点D交BC于点M，BD=EF．求证：BM=EM．
证明：∵ED⊥AB于点D，EF⊥BC于点F，
∴∠BDM=∠MFE=90°．
在△BDM和△EFM中
，
∴△BDM≌△EFM（AAS），
∴BM=EM（全等三角形对应边相等）．
分析：求出∠BDM=∠MFE=90°，根据AAS证△BDM≌△EFM，根据全等三角形的性质推出即可．
点评：本题考查了全等三角形的性质和判定的应用，主要考查学生的推理能力．
∴∠BDM=∠MFE=90°．
在△BDM和△EFM中
，∴△BDM≌△EFM（AAS），
∴BM=EM（全等三角形对应边相等）．
分析：求出∠BDM=∠MFE=90°，根据AAS证△BDM≌△EFM，根据全等三角形的性质推出即可．
点评：本题考查了全等三角形的性质和判定的应用，主要考查学生的推理能力．
练习册系列答案
相关题目
23、看图填空：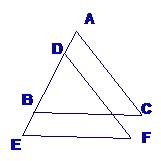
23、已知：如图BC∥EF，BC=EF，AB=DE；说明AC与EF相等．
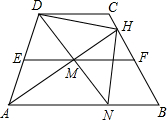（2008•攀枝花）已知：如图，EF为梯形ABCD的中位线，AD=AN，连接DN交EF于点M，AM的延长线交BC于点H，连接DH、NH
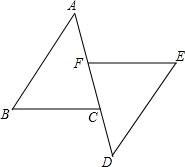已知：如图，EF∥BC，点F，点C在AD上，BC=EF，AC=DF．
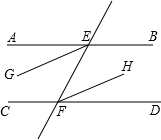已知：如图，EF分别交于AB、CD于E、F，∠AEF=∠EFD，EG平分∠AEF，FH平分∠EFD．试说明EG∥FH成立的理由．