题目内容

23、看图填空：
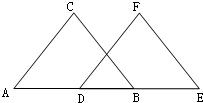
已知：如图，EF⊥BC，AD⊥BC，∠1=∠2，∠BAC=80°．求∠AMD的度数．
解：∵EF⊥BC，AD⊥BC
∴AD∥EF
∴∠

=∠

∵∠1=∠2
∴∠2=

∠3

∴AB∥DM
∴∠

BAC

+∠

AMD

=180°
∵∠BAC=80°
∴∠AMD=

100°

．

分析：首先由EF⊥BC，AD⊥BC，推出AD∥EF，得∠1=∠3，再由已知∠1=∠2得∠2=∠3，所以推出AB∥DM，则根据两直线平行同旁内角互补，求出∠AMD的度数．

解答：解：：∵EF⊥BC，AD⊥BC
∴AD∥EF
∴∠1=∠3，
∵∠1=∠2
∴∠2=∠3，
∴AB∥DM，
∴∠BAC+∠AMD=180°，
∴∠AMD=180°-∠BAC=180°-80°=100°，
故答案分别为：∠1，，∠3，，∠3，BAC，ADM，100°．

点评：此题考查的知识点是平行线的判定与性质，解题的关键是由已知先证AB∥DM，再根据两直线平行同旁内角互补，求出∠AMD的度数．

练习册系列答案

相关题目

20、看图填空：
已知：如图，BC∥EF，AD=BE，BC=EF．
试说明△ABC≌△DEF．
解：∵AD=BE
∴

（两直线平行，同位角相等）
在△ABC和△DEF中，

AB=DE，∠ABC=∠DEF，BC=EF，

∴△ABC≌△DEF（SAS）．

看图填空：
已知：如图，BC∥EF，AD=BE，BC=EF，试说明 AC=DF
解：∵AD=BE
∴AD+DB=BE+

看图填空：
已知：如图，BC∥EF，AD=BE，BC=EF，试说明 AC=DF
解：∵AD=BE
∴AD+DB=BE+（等式的性质）
即：AB=
∵BC∥EF
∴∠ABC=∠（）
在△ABC和△DEF中
$数学公式$
∴△ABC≌△DEF（）
∴AC=DF （）．

看图填空：
已知：如图，BC∥EF，AD=BE，BC=EF，试说明△ABC ≌ △DEF。
解：∵AD=BE，
       ∴____=BE+DB，
        即：_____=_____，
       ∵BC∥ EF，
        ∴∠_____=∠_____，（           ）
      在△ABC和△DEF中，
        ________________ ，
         ________________，
        ________________ ，
        ∴△ABC ≌ △DEF。（SAS）

看图填空：已知：如图，BC∥EF，AD=BE，BC=EF，试说明 AC=DF解：∵AD=BE∴AD+DB=BE+________（等式的性质）即：AB=________∵BC∥EF∴∠ABC=∠________（________）在△ABC和△DEF中∴△ABC≌△DEF（________）∴AC=DF （________）．

试题分类

看图填空：
已知：如图，BC∥EF，AD=BE，BC=EF，试说明 AC=DF
解：∵AD=BE
∴AD+DB=BE+（等式的性质）
即：AB=
∵BC∥EF
∴∠ABC=∠（）
在△ABC和△DEF中
$数学公式$
∴△ABC≌△DEF（）
∴AC=DF （）．