题目内容
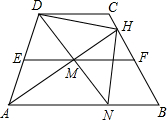（2008•攀枝花）已知：如图，EF为梯形ABCD的中位线，AD=AN，连接DN交EF于点M，AM的延长线交BC于点H，连接DH、NH（1）给出以下结论：
①AH⊥DN；②AD⊥DH；③HM=MN；④DH=NH
你认为正确的结论是
①④
①④
．（2）请任意选择（1）中的一个正确结论加以证明．
分析：（1）①④正确；
（2）首先根据中位线的性质可得EF∥AB，进而可得△DEM∽△DAN，再根据对应边成比例可得到M为DN中点，再有AD=AN，可根据等腰三角形的性质可得AH⊥DN；再根据线段垂直平分线的性质可证出④正确．
（2）首先根据中位线的性质可得EF∥AB，进而可得△DEM∽△DAN，再根据对应边成比例可得到M为DN中点，再有AD=AN，可根据等腰三角形的性质可得AH⊥DN；再根据线段垂直平分线的性质可证出④正确．
解答：解：（1）①④正确；
（2）∵EF为梯形ABCD的中位线，
∴EF∥AB，
∴△DEM∽△DAN，
∴
=
，
∵E为AD中点，
∴
=
，
∴
=
，
∴M为DN中点，
∵AD=AN，
∴AH⊥DN，故①正确；
∵AH⊥DN，M为DN中点，
∴HM是DN的垂直平分线，
∴DH=HN，故④正确．
（2）∵EF为梯形ABCD的中位线，
∴EF∥AB，
∴△DEM∽△DAN，
∴
| DE |
| DA |
| DM |
| DN |
∵E为AD中点，
∴
| DE |
| AD |
| 1 |
| 2 |
∴
| DM |
| DN |
| 1 |
| 2 |
∴M为DN中点，
∵AD=AN，
∴AH⊥DN，故①正确；
∵AH⊥DN，M为DN中点，
∴HM是DN的垂直平分线，
∴DH=HN，故④正确．
点评：此题主要考查了梯形的中位线，以及等腰三角形的性质，线段的垂直平分线，关键是掌握等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
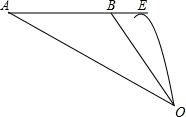60°．飞机继续飞行0.1千米到达E处进行空投，已知空投物资在空中下落过程中的轨迹是抛物线，若要使空投物资刚好落在O处．